Cuantos angulos tiene un rombo
Propiedades del rombo
En la geometría euclidiana plana, un rombo (plural rombos o rhombuses) es un cuadrilátero cuyos cuatro lados tienen la misma longitud. Otro nombre es cuadrilátero equilátero, ya que equilátero significa que todos sus lados tienen la misma longitud. El rombo suele llamarse diamante, por el palo de los diamantes en los naipes, que se asemeja a la proyección de un diamante octaédrico, o rombo, aunque el primero a veces se refiere específicamente a un rombo con un ángulo de 60° (que algunos autores llaman calisson por el dulce francés[1] – véase también Poliamante), y el segundo a veces se refiere específicamente a un rombo con un ángulo de 45°.
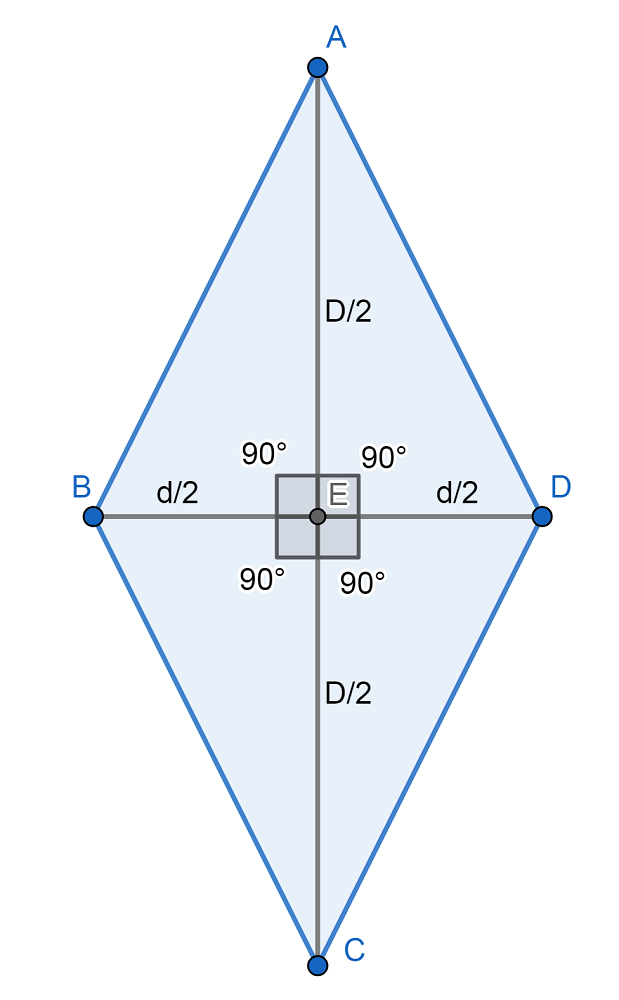
Todo rombo tiene dos diagonales que conectan pares de vértices opuestos y dos pares de lados paralelos. Utilizando triángulos congruentes, se puede demostrar que el rombo es simétrico a través de cada una de estas diagonales. Se deduce que todo rombo tiene las siguientes propiedades:
La primera propiedad implica que todo rombo es un paralelogramo. Por tanto, un rombo tiene todas las propiedades de un paralelogramo: por ejemplo, los lados opuestos son paralelos; los ángulos adyacentes son suplementarios; las dos diagonales se bisecan entre sí; cualquier línea que pase por el punto medio biseca el área; y la suma de los cuadrados de los lados es igual a la suma de los cuadrados de las diagonales (ley del paralelogramo). Así, denotando el lado común como a y las diagonales como p y q, en todo rombo
Cuadrado
Explicación: Los cuatro ángulos interiores de cualquier rombo deben tener una suma de grados. Los ángulos interiores opuestos deben ser equivalentes, y los ángulos adyacentes tienen una suma de grados. Así, si un rombo tiene dos ángulos interiores de grados, también debe haber dos ángulos que sean iguales: Comprueba:
Los ángulos interiores opuestos deben ser equivalentes, y los ángulos adyacentes tienen una suma de grados. Dado que, tanto los ángulos y son adyacentes al ángulo –hallar la medida de uno de estos dos ángulos por: El ángulo y debe ser cada uno igual a los grados. Así que la suma de los ángulos y grados.
Explicación: Un rombo se define como un paralelogramo con cuatro lados congruentes; no hay ninguna restricción en cuanto a las medidas de los ángulos. Por lo tanto, un rombo puede tener ángulos de cualquier medida. La opción correcta es “falso”.
Tutores de ISEE en Miami, Tutores de Inglés en Washington DC, Tutores de Informática en Washington DC, Tutores de Español en Miami, Tutores de ISEE en Filadelfia, Tutores de SSAT en Dallas Fort Worth, Tutores de GRE en Filadelfia, Tutores de SAT en Filadelfia, Tutores de Biología en Denver, Tutores de Física en Washington DC
¿es un cuadrado un rombo
congruente. ¡Simulación interactiva el acertijo matemático más controvertido de la historia! Los 4 lados son congruentes. Pregúntate: ¿Qué hay de cierto en los ángulos formados por las diagonales de un rombo? ¿Cómo puedes utilizar el hecho de que los lados de un rombo
Una pantalla de cristal líquido (LCD) es una pantalla plana u otro dispositivo óptico modulado electrónicamente que utiliza las propiedades de modulación de la luz de los cristales líquidos combinados con polarizadores.Los cristales líquidos no emiten luz directamente, sino que utilizan una luz de fondo o un reflector para producir imágenes en color o monocromas. En este artículo vamos a calcular el área de una forma L (formada por 2 rectángulos).
Sección 4 – Los impares 1. Como 1.000.000 = 2 6 × 5 6, el número de lados no es un producto de primos de Fermat distintos y una potencia de dos. El rombo. 10. Así es como se puede detener al barrenador esmeralda del fresno (BEF) antes de que esta plaga invasora destruya más bosques.
Esta es una pregunta bastante ridícula para los estudiantes de segundo grado. Android Inc. fue fundada en Palo Alto, California, en octubre de 2003 por Andy Rubin, Rich Miner, Nick Sears y Chris White. A lo largo de la segunda mitad del siglo XX, las mujeres estadounidenses participaron en la fuerza de trabajo a un ritmo creciente.
Cometa
La argumentación lógica, las definiciones precisas y las pruebas claras son esenciales para entender las matemáticas. Estas habilidades analíticas pueden trasladarse a muchos ámbitos del comercio, la ingeniería, la ciencia y la medicina, pero la mayoría de nosotros las encontramos por primera vez en las matemáticas de la escuela secundaria.
Aparte de algunos resultados de la teoría de los números, como la existencia de un número infinito de primos y el Teorema Fundamental de la Aritmética, la mayoría de los teoremas que conocen los estudiantes son de geometría, empezando por el teorema de Pitágoras.
Al igual que en el módulo Paralelogramos y Rectángulos, en este módulo se insiste primero en las definiciones precisas de cada cuadrilátero especial, luego se desarrollan algunas de sus propiedades y, a continuación, se invierte el proceso, examinando si estas propiedades pueden utilizarse como pruebas para ese cuadrilátero especial en particular. Hemos visto que una prueba para un cuadrilátero especial suele ser la inversa de una propiedad. Por ejemplo, un par típico de propiedad-prueba del módulo anterior es el par de afirmaciones inversas:
Varios de los teoremas demostrados en este módulo se basan en uno o varios de los teoremas anteriores del módulo. Esto significa que el lector debe comprender toda una “secuencia de teoremas” para obtener algunos resultados. Esto es típico de las matemáticas más avanzadas.