Triangulo rectangulo trigonometria
Contenidos
Triangulo rectangulo trigonometria en línea
Si se aceptan las definiciones de las funciones trigonométricas introducidas por los matemáticos en un triángulo rectangular, los valores de estas funciones dependen únicamente de la relación de los tamaños de las partes de un triángulo. El tamaño de los ángulos en un triángulo rectangular está en el rango de los ángulos trigonométricos. Las funciones trigonométricas no tienen signos y no poseen periodicidad. Estas propiedades son elementos del homocentrismo.
La matemática del homocentrismo es una matemática en la que el resultado depende de la opción de la matemática relativa aceptada por nosotros o de nuestra opinión. Ejemplos llamativos de un homocentrismo en matemáticas son: la división de los números en positivo y en negativo, la numeración decimal, los números y los números inversos, el sistema de coordenadas cartesianas, etc.
Esta definición es posible sólo porque para cualquier punto de un círculo de coordenadas se utilizan como elementos de relleno para la creación de un triángulo rectangular. Para los puntos transversales de un círculo y la creación de coordenadas de un triángulo es imposible.
Para cualquier punto del plano en el sistema de coordenadas cartesianas las funciones trigonométricas se pueden definir como la relación de coordenadas de este punto o la relación de coordenadas de un punto a la distancia de un punto al centro de un marco. Una excepción es el punto transversal de coordenadas (el centro de un marco) para el que no se pueden definir funciones trigonométricas. Este hecho es un defecto congénito del sistema de coordenadas cartesianas. Si es necesario definir funciones trigonométricas para el punto que coincide con el centro de un marco, entonces el marco necesita ser desplazado a un lado.
Triangulo rectangulo trigonometria del momento
Volvamos a la convención estándar para etiquetar las partes de un triángulo rectángulo. El ángulo recto se llama C y la hipotenusa c. A y B son los otros dos ángulos, y a y b los lados opuestos a ellos, respectivamente.
Veamos primero algunos casos en los que no conocemos todos los lados. Supongamos que no conocemos la hipotenusa pero sí los otros dos lados. El teorema de Pitágoras nos dará la hipotenusa. Por ejemplo, si a = 10 y b = 24, entonces c2 = a2 + b2 = 102 + 242 = 100 + 576 = 676. La raíz cuadrada de 676 es 26, así que c = 26. (Es bonito dar ejemplos en los que las raíces cuadradas salen números enteros; en la vida normalmente no lo hacen).
Supongamos ahora que conocemos la hipotenusa y un lado, pero tenemos que encontrar el otro. Por ejemplo, si b = 119 y c = 169, entonces a2 = c2 – b2 = 1692 – 1192 = 28561 – 14161 = 14400, y la raíz cuadrada de 14400 es 120, así que a = 120.
Es posible que sólo conozcamos un lado pero que también conozcamos un ángulo. Por ejemplo, si el lado a = 15 y el ángulo A = 41°, podemos usar un seno y una tangente para encontrar la hipotenusa y el otro lado. Como sin A = a/c, sabemos que c = a/sin A = 15/sin 41. Usando una calculadora, esto es 15/0,6561 = 22,864. Además, tan A = a/b, por lo que b = a/tan A = 15/tan 41 = 15/0,8693 = 17,256. El uso de un seno, coseno o tangente depende del lado y el ángulo que conozcas.
Triangulo rectangulo trigonometria 2020
RESOLVER UN TRIÁNGULO significa conocer los tres lados y los tres ángulos. Cuando conocemos las proporciones de los lados, utilizamos el método de las figuras semejantes. Ese es el método que hay que utilizar para resolver un triángulo rectángulo isósceles o un triángulo 30°-60°-90°. Cuando no conozcamos los números de las razones, debemos utilizar la tabla de razones. El siguiente ejemplo ilustra cómo hacerlo.
Solución. El ángulo de depresión es el ángulo por debajo de la recta -horizontal- que debe mirar un observador para ver algo por debajo del observador. Así, para ver el barco, el farero debe mirar 6° hacia abajo.
Ahora bien, el triángulo formado por el faro y la distancia d del barco con respecto al faro, es un ángulo recto. Y como el ángulo de depresión es de 6°, entonces el ángulo alterno es también de 6°. (Euclides, I. 29.)
Trigonometría: encontrar ángulos en triángulos rectángulos
Estas fórmulas relacionan longitudes y áreas de determinados círculos o triángulos. En la página siguiente encontrarás las identidades. Las identidades no se refieren a figuras geométricas concretas, sino que valen para todos los ángulos.
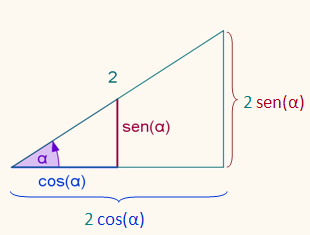
Las fórmulas más importantes de la trigonometría son las del triángulo rectángulo. Si θ es uno de los ángulos agudos de un triángulo, el seno de theta es la relación entre el lado opuesto y la hipotenusa, el coseno es la relación entre el lado adyacente y la hipotenusa, y la tangente es la relación entre el lado opuesto y el adyacente.
Estas tres fórmulas se conocen colectivamente con el mnemónico SohCahToa. Además de éstas, existe la importantísima fórmula pitagórica que dice que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados.
Estas fórmulas sirven para cualquier triángulo, ya sea agudo, obtuso o rectángulo. Utilizaremos la notación estándar, en la que los tres vértices del triángulo se indican con las letras mayúsculas A, B y C, mientras que los tres lados opuestos a ellos se indican respectivamente con las letras minúsculas a, b y c.