Cuál es el mínimo común múltiplo
Contenidos
Lcm para principiantes (versión antigua)
Este artículo está escrito como un manual o guía. Por favor, ayude a reescribir este artículo desde un punto de vista descriptivo y neutral, y elimine los consejos o instrucciones. (Febrero de 2020) (Aprende cómo y cuándo eliminar este mensaje de la plantilla)
Diagrama de Venn que muestra los múltiplos mínimos comunes de las combinaciones de 2, 3, 4, 5 y 7 (el 6 se omite porque es 2 × 3, ambos ya representados).Por ejemplo, un juego de cartas que requiere que sus cartas se dividan en partes iguales entre un máximo de 5 jugadores requiere al menos 60 cartas, el número en la intersección de los conjuntos 2, 3, 4 y 5, pero no el conjunto 7.
En aritmética y teoría de los números, el mínimo común múltiplo, mínimo común múltiplo o mínimo común múltiplo de dos enteros a y b, normalmente denotado por lcm(a, b), es el menor número entero positivo que es divisible por a y b. 1][2][3] Dado que la división de enteros por cero no está definida, esta definición sólo tiene sentido si a y b son distintos de cero[4]. Sin embargo, algunos autores definen lcm(a,0) como 0 para todo a, que es el resultado de tomar el lcm como el menor límite superior en la red de divisibilidad.
Cuál es el mínimo común múltiplo 2021
Este artículo está escrito como un manual o guía. Por favor, ayude a reescribir este artículo desde un punto de vista descriptivo y neutral, y elimine los consejos o instrucciones. (Febrero de 2020) (Aprende cómo y cuándo eliminar este mensaje de la plantilla)
Diagrama de Venn que muestra los múltiplos mínimos comunes de las combinaciones de 2, 3, 4, 5 y 7 (el 6 se omite porque es 2 × 3, ambos ya representados).Por ejemplo, un juego de cartas que requiere que sus cartas se dividan en partes iguales entre un máximo de 5 jugadores requiere al menos 60 cartas, el número en la intersección de los conjuntos 2, 3, 4 y 5, pero no el conjunto 7.
En aritmética y teoría de los números, el mínimo común múltiplo, mínimo común múltiplo o mínimo común múltiplo de dos enteros a y b, normalmente denotado por lcm(a, b), es el menor número entero positivo que es divisible por a y b. 1][2][3] Dado que la división de enteros por cero no está definida, esta definición sólo tiene sentido si a y b son distintos de cero[4]. Sin embargo, algunos autores definen lcm(a,0) como 0 para todo a, que es el resultado de tomar el lcm como el menor límite superior en la red de divisibilidad.
Cuál es el mínimo común múltiplo online
En matemáticas, el mínimo común múltiplo, también conocido como el mínimo común múltiplo de dos (o más) números enteros a y b, es el menor número entero positivo que es divisible por ambos. Se suele denominar LCM(a, b).
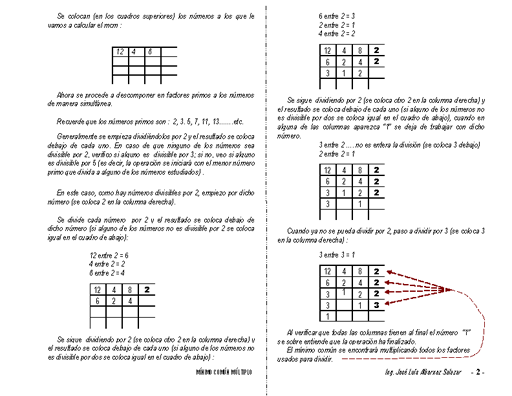
Una forma más sistemática de encontrar el MCL de algunos enteros dados es utilizar la factorización de primos. La factorización de primos implica descomponer cada uno de los números que se comparan en su producto de números primos. El MCL se determina entonces multiplicando la potencia más alta de cada número primo. Tenga en cuenta que calcular el MCL de esta manera, aunque es más eficiente que usar el método de “fuerza bruta”, sigue estando limitado a los números más pequeños. Consulte el ejemplo siguiente para aclarar cómo utilizar la factorización de primos para determinar el MCL:
Un tercer método viable para encontrar el MCL de algunos enteros dados es usar el máximo común divisor. Este método también se conoce como el mayor factor común (GCF), entre otros nombres. Consulte el enlace para obtener detalles sobre cómo determinar el máximo común divisor. Dado LCM(a, b), el procedimiento para encontrar el LCM usando GCF es dividir el producto de los números a y b por su GCF, es decir, (a × b)/GCF(a,b). Cuando se trata de determinar el MCL de más de dos números, por ejemplo LCM(a, b, c) se encuentra el MCL de a y b donde el resultado será q. Luego se encuentra el MCL de c y q. El resultado será el MCL de los tres números. Utilizando el ejemplo anterior:
Cuál es el mínimo común múltiplo del momento
Relacionando esta definición con el problema que hemos resuelto en la página anterior, vemos que los dos números n y m son los números 12 y 20. Podemos escribir la solución simbólicamente como LCM(12, 20) = 60. Esto dice “el mínimo común múltiplo de 12 y 20 es 60”.
Como hemos encontrado el mínimo común múltiplo, 60, para el problema de los engranajes, ahora podemos responder a la pregunta del problema de los engranajes. La pregunta se refería a cuántas revoluciones son necesarias para realinear la marca. Como sabemos que el primer engranaje debe pasar 60 dientes y que cada 12 ha hecho una revolución, sabemos que debe hacer 5 revoluciones antes de que las marcas se alineen por primera vez (60 ÷ 12 = 5). (También hay que tener en cuenta que el segundo engranaje debe hacer tres revoluciones para que los 60 dientes pasen por la marca, 60 ÷ 20 = 3).
Como estamos buscando múltiplos, cada múltiplo de 308 debe contener 22 – 7 – 11 como factores y cada múltiplo de 1176 debe contener 23 – 3 – 72 como factores. Esto significa que 2, 3, 7 y 11 deben ser factores primos en cualquier múltiplo común. Para 2 y 7, que aparecen en ambas listas, necesitamos la potencia más alta de ese primo como factor para crear el MCL, ya que 23 es automáticamente un múltiplo de 22. Así que utilizando la potencia más alta de cada primo, LCM (308,1176) = 23 – 3 – 72 – 11 = 12,936.