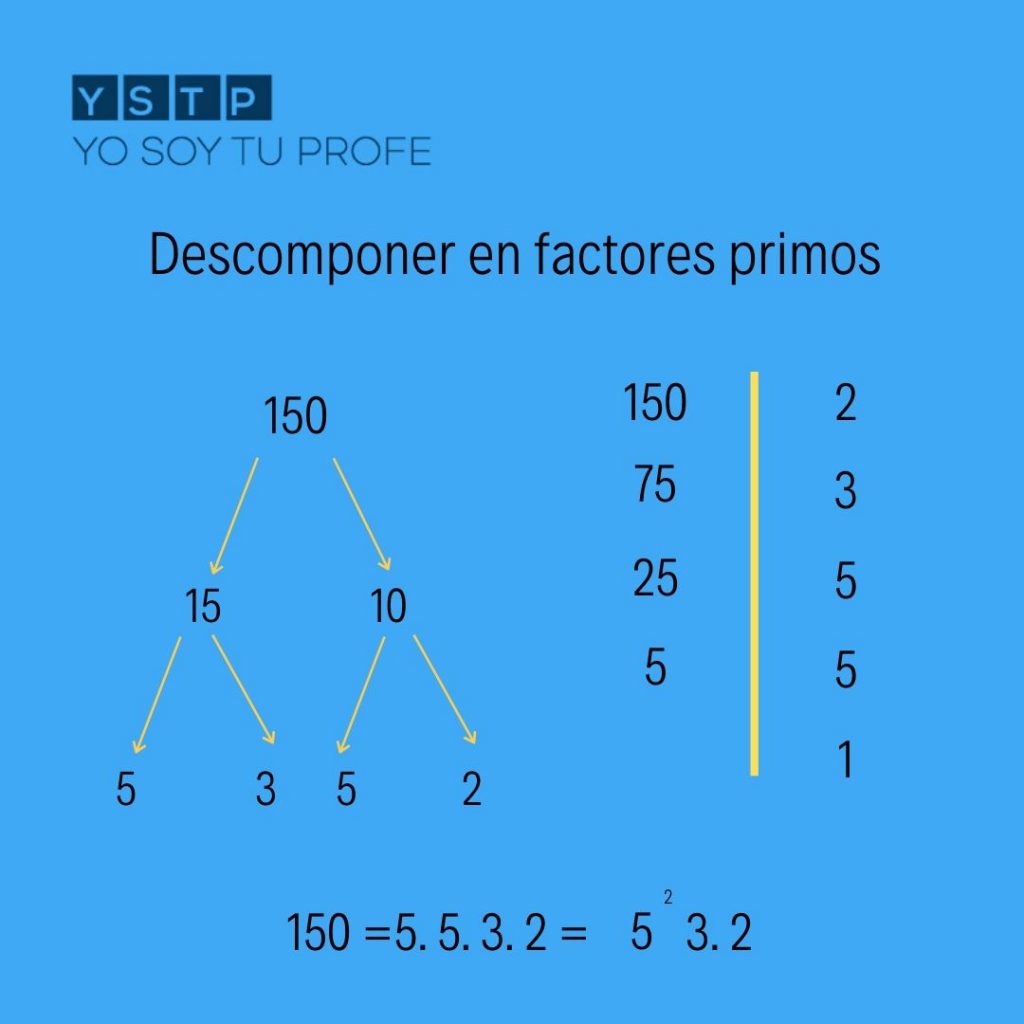
Descomponer en factores primos ejercicios
Contenidos
Ejercicios de factorización de números primos
Los números primos son números naturales (números enteros positivos que a veces incluyen el 0 en ciertas definiciones) mayores que 1, que no pueden formarse multiplicando dos números menores. Un ejemplo de número primo es el 7, ya que sólo se puede formar multiplicando los números 1 y 7. Otros ejemplos son 2, 3, 5, 11, etc.
Los números primos son muy utilizados en la teoría de los números debido al teorema fundamental de la aritmética. Este teorema establece que los números naturales mayores que 1 son primos o pueden ser factorizados como un producto de números primos. Por ejemplo, el número 60 puede ser factorizado en un producto de números primos de la siguiente manera:
Un método para encontrar los factores primos de un número compuesto es la división de prueba. La división de prueba es uno de los algoritmos más básicos, aunque es muy tedioso. Consiste en probar cada número entero dividiendo el número compuesto en cuestión por el número entero, y determinar si, y cuántas veces, el número entero puede dividir el número uniformemente. Como ejemplo sencillo, a continuación se muestra la factorización en primo de 820 utilizando la división de prueba:
Comentarios
Una de las razones por las que estudiamos los múltiplos y los primos es para utilizar estas técnicas para encontrar el mínimo común múltiplo de dos números. Esto será útil cuando sumemos y restemos fracciones con diferentes denominadores.
Un múltiplo común de dos números es un número que es múltiplo de ambos números. Supongamos que queremos encontrar los múltiplos comunes de 10 y 25. Podemos enumerar los primeros múltiplos de cada número. A continuación, buscamos los múltiplos que son comunes a ambas listas: son los múltiplos comunes.
El número más pequeño que aparece en ambas listas es \(60\), por lo que \(60\) es el mínimo común múltiplo de \(15\) y \(20\). Fíjate que \(120\) también está en ambas listas. Es un múltiplo común, pero no es el mínimo común múltiplo.
Observa que los factores primos de \(12\) y los factores primos de \(18\) están incluidos en el MCL. Al hacer coincidir los primos comunes, cada factor primo común se utiliza sólo una vez. Esto asegura que \(36\) es el mínimo común múltiplo.
Calculadora de factorización de primos
La teoría de los números -el estudio de los números enteros- ha fascinado a los matemáticos durante años. Los números enteros son fundamentales para la teoría de los números: 0, 1, 2, 3, etc. Los componentes básicos de todos los números enteros son los números primos. Un número primo es un número entero que sólo tiene dos factores: él mismo y el uno. Cuando un número tiene más de dos factores, se dice que es un número compuesto.
Los números uno y cero son casos inusuales. El número uno sólo tiene un factor y no se considera ni primo ni compuesto. El número cero tiene un número infinito de factores, ya que el cero puede ser dividido uniformemente por cualquier cosa excepto por el cero. Por esta razón, el cero tampoco se considera primo ni compuesto.
Los alumnos de 4º curso en adelante suelen estar preparados para aprender sobre los factores primos, y los de 6º curso en adelante suelen estar preparados para investigar la factorización primaria de un número y explorar cómo puede utilizarse para generar todos los números enteros.
Cuando un número compuesto se escribe como producto de todos sus factores primos, tenemos la factorización primaria del número. Así, si escribimos 36 como producto de todos sus factores primos, podemos encontrar la factorización primaria de 36.
Cómo hacer la factorización de primos
Este es un nuevo tipo de actividad en el que estoy trabajando, con el pegadizo nombre de Rellena los huecos. Es mi intento de replicar algunas de mis actividades favoritas de clasificación de tarjetas de las Unidades de Estándares, pero con menos recortes y algunos elementos de variación.
Aunque sigue encajando en mi definición de Práctica Inteligente (y como tal, las notas de orientación para llevar a cabo este tipo de actividades deberían seguir siendo útiles), las veo más como una actividad de revisión. Las utilizo como una forma de reunir varios conceptos, desafiando a los estudiantes a trabajar hacia adelante y hacia atrás a través de filas, para asegurarse de que no se atan a una sola forma de pensar.
He animado el PowerPoint para que se pueda hacer clic en las casillas en cualquier orden para revelar cada respuesta. Esto permite que los estudiantes describan el orden en que resolvieron cada problema durante el debate en clase.
Es fascinante ver a los alumnos trabajar con ellos. La mayoría centra su atención en la página, moviéndose hacia delante y hacia atrás en cada fila. En el debate de toda la clase que sigue, puedo dirigir su atención a las relaciones que existen entre las filas.