Numeros primos y numeros compuestos

Lista de números compuestos

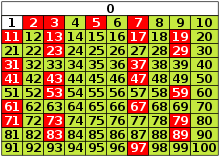
Pre-álgebra> Números primos y compuestos <Números primos y compuestosFactores:  Los factores son números que se multiplican para obtener un producto.    En la frase de multiplicación3X7=21, los factores de 21 son 3 y 7.Números primos:  Los números que sólo tienen dos factores, 1 y él mismo, se llaman números primos. Ejemplo: el número 5 es un número primo. No se puede dividir 5 uniformemente entre 2, 3 o 4. Sólo se puede dividir 5 en partes iguales por 1 o por sí mismo.  Números compuestos:  Los números que tienen más de 2 factores se llaman números compuestos. El número 6 es un ejemplo de número compuesto. Puedes dividir el 6 en partes iguales entre 1, 2, 3 y 6. La siguiente tabla muestra algunos ejemplos de números primos y compuestos.  Los números primos son azules. Los números compuestos están en negro.

Comentarios

Los números primos han atraído la atención del ser humano desde los primeros tiempos de la civilización. Explicamos qué son, por qué su estudio entusiasma a matemáticos y aficionados por igual, y de paso abrimos una ventana al mundo de los matemáticos.
Desde el principio de la historia de la humanidad, los números primos despertaron la curiosidad humana. ¿Qué son? ¿Por qué son tan difíciles las preguntas relacionadas con ellos? Una de las cosas más interesantes de los números primos es su distribución entre los números naturales. A pequeña escala, la aparición de los números primos parece aleatoria, pero a gran escala parece haber un patrón, que aún no se entiende del todo. En este breve artículo, intentaremos seguir la historia de los números primos desde la antigüedad y aprovechar esta oportunidad para sumergirnos y comprender mejor el mundo de los matemáticos.
¿Se ha preguntado alguna vez por qué el día se divide exactamente en 24 h, y el círculo en 360 grados? El número 24 tiene una interesante propiedad: puede dividirse en partes enteras iguales de un número relativamente grande de maneras. Por ejemplo, 24÷2 = 12, 24÷3 = 8, 24÷4 = 6, y así sucesivamente (¡completa tú mismo el resto de opciones!). Esto significa que un día puede dividirse en dos partes iguales de 12 h cada una, la diurna y la nocturna. En una fábrica que trabaja sin parar en turnos de 8 h, cada día se divide exactamente en tres turnos.

Aerle.es

Tabla de números primos y compuestos

Un número primo (o primo) es un número natural mayor que 1 que no es producto de dos números naturales menores. Un número natural mayor que 1 que no es primo se llama número compuesto. Por ejemplo, el 5 es primo porque las únicas formas de escribirlo como producto, 1 × 5 o 5 × 1, implican al propio 5.
Sin embargo, el 4 es compuesto porque es un producto (2 × 2) en el que ambos números son menores que el 4. Los primos son fundamentales en la teoría de los números debido al teorema fundamental de la aritmética: todo número natural mayor que 1 es un primo en sí mismo o puede ser factorizado como un producto de primos que es único hasta su orden.
. Entre los algoritmos más rápidos se encuentran el test de primalidad de Miller-Rabin, que es rápido pero tiene una pequeña posibilidad de error, y el test de primalidad de AKS, que siempre produce la respuesta correcta en tiempo polinómico pero es demasiado lento para ser práctico. Existen métodos particularmente rápidos para números de formas especiales, como los números de Mersenne. En diciembre de 2018[actualización] el mayor número primo conocido es un primo de Mersenne con 24.862.048 dígitos decimales[1].

Lista de números primos y números compuestos

En el apartado anterior hemos encontrado los factores de un número. Los números primos sólo tienen dos factores, el número [latex]1[/latex] y el propio número primo. Los números compuestos tienen más de dos factores, y cada número compuesto puede escribirse como un único producto de primos. Esto se llama la factorización primaria de un número. Cuando escribimos la factorización primaria de un número, estamos reescribiendo el número como un producto de primos. Encontrar la factorización primaria de un número compuesto te ayudará más adelante en este curso.
Una forma de encontrar la factorización primaria de un número es hacer un árbol de factores. Comenzamos escribiendo el número y luego lo escribimos como el producto de dos factores. Escribimos los factores debajo del número y los conectamos al número con un pequeño segmento de línea, una “rama” del árbol de factores.
Si un factor es primo, lo rodeamos (como un brote en un árbol), y no factorizamos más esa “rama”. Si un factor no es primo, repetimos este proceso, escribiéndolo como el producto de dos factores y añadiendo nuevas ramas al árbol.