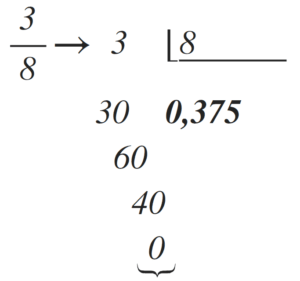Fraccion decimal a numero decimal
Contenidos
Convertidor de fracciones a decimales
Una forma fácil de convertir una fracción en decimal¿Estás listo para aprender a convertir una fracción en un decimal?(Haz clic aquí para aprender a hacer lo contrario y convertir un decimal en una fracción)Antes de aprender una forma fácil de convertir una fracción en un decimal (con y sin calculadora), necesitas entender qué son los decimales y las fracciones:
La clave de estas definiciones es que los decimales y las fracciones son diferentes formas de representar la misma cosa: un número que no es entero. Cómo convertir una fracción en decimalPuedes convertir fácilmente una fracción en un decimal utilizando algunas estrategias sencillas:1.) Utilizando una calculadoraLa forma más fácil de convertir una fracción en un decimal es dividir el numerador (la parte superior de la fracción) entre el denominador (la parte inferior de la fracción) utilizando una calculadora. La respuesta resultante será el valor de la fracción expresado como un número decimal.Por ejemplo, para convertir la fracción 7/8 a un decimal usando una calculadora, simplemente ejecute 7 dividido por 8 y presione enter. El decimal resultante sería 0,875.Por lo tanto, se puede decir que 7/8 expresado como decimal es 0,875
Manera fácil de convertir una fracción en decimal
fracciones reducidas con d como denominador. El tamaño de la parte recurrente viene determinado por el resto de la factorización del denominador, E. 1/E será puramente recurrente y la longitud de su período es la misma que la de la parte recurrente
1/n terminando en bases 2 a 12 Base:1/21/31/41/51/61/71/81/91/101/111/12 20.10.[01]0.010.[0011]0.0[01]0.[001]0.0010.[000111]0.0[0011]0.[0001011101]0. 00[01] 30.[1]0.10.[02]0.[0121]0.0[1]0.[010212]0.[01]0.010.[0022]0.[00211]0.0[02] 40.20.[1]0.10.[03]0.0[2]0.[021]0.020.[013]0.0[12]0.[01131]0.0[1] 50.[2]0.[13]0. [1]0.10.[04]0.[032412]0.[03]0.[023421]0.0[2]0.[02114]0.[02] 60.30.20.130.[1]0.10.[05]0.0430.040.0[3]0.[0313452421]0.03 70.[3]0.[2]0.[15]0.[1254]0.[1]0.10. [06]0.[053]0.[0462]0.[0431162355]0.[04] 80.40.[25]0.20.[1463]0.1[25]0.[1]0.10.[07]0.0[6314]0.[0564272135]0.0[52] 90.[4]0.30.[2]0.[17]0.1[4]0.[125]0.[1]0.10. [08]0.[07324]0.0[6] 100.50.[3]0.250.20.1[6]0.[142857]0.1250.[1]0.10.[09]0.08[3] 110.[5]0.[37]0.[28]0.[2]0.[19]0.[163]0.[14]0.[124986]0.[1]0.10.[0A] 120.60. 40.30.[2497]0.20.[186A35]0.160.140.1[2497]0.[1]0.1 130.[6]0.[4]0.[3]0.[27A5]0.[2]0.[1B]0.[18]0.[15A]0.[13B9]0.[12495BA837]0.[1] 140.70.[49]0.370.[2B]0.2[49]0. 20.1A70.[17AC63]0.1[58]0.[13B65]0.12[49] 150.[7]0.50.[3B]0.30.2[7]0.[2]0.[1D]0.1A0.1[7]0.[156C4]0.1[3B] 160.80.[5]0.40.[3]0.2[A]0.[249]0.20.[1C7]0.1[9]0. [1745D]0.1[5] 170.[8]0.[5B]0.[4]0.[36DA]0.[2E]0.[274E9C]0.[2]0.[1F]0.[1BF5]0.[194ADF7C63]0.[17] 180.90.60.490.[3AE7]0.30.[2A5]0.2490.20.1[E73A]0.[1B834G69ED]
Hoja de trabajo de conversión de fracciones a decimales
Cuenta la leyenda que la primera persona de la antigua Grecia que descubrió que hay números que no se pueden escribir como fracciones fue arrojada por la borda de un barco. Siglos después, aunque utilizamos habitualmente números que no se pueden escribir como fracciones, los números que sí se pueden escribir como fracciones siguen siendo herramientas poderosas. ¿Qué hace que las fracciones sean tan especiales? Exploramos cómo podemos reconocer la representación decimal de las fracciones y cómo las fracciones pueden utilizarse para aproximar cualquier número real tanto como queramos.
El lunes por la mañana, tu amigo Jordan se acerca a ti y te dice: “Estoy pensando en un número entre 1 y 100”. Como buen deportista, le sigues la corriente y adivinas el 43. “¡No, demasiado bajo!” declara Jordan. “Bien, ¿qué tal el 82?”, preguntas. “¡Demasiado alto!” responde Jordan. Sigues adivinando. 60 es demasiado bajo. 76 es demasiado alto. 70 es demasiado bajo. Sintiéndote satisfecho de que te estás acercando, preguntas: “¿Qué tal 75?”. “¡Lo tienes!” responde Jordan, y te diriges triunfante a tu primera clase del día.
Pero después de la clase, vuelves a encontrarte con Jordan, que al parecer ha estado pensando en formas de dejarte perplejo: ¿por qué limitarse a los números positivos? ¿Y si también se permiten los números negativos? “Ahora estoy pensando en un número entre el 100 negativo y el 100”, dice Jordan alegremente. Decides picar el anzuelo, y rápidamente descubres que esto no cambia mucho el juego. Adivinas, y al ir subiendo y bajando te vas acercando cada vez más al objetivo. Si el número de Jordan es -32, y ya has averiguado que -33 es demasiado bajo y -31 demasiado alto, entonces sabes que la respuesta es -32. Pero entonces te das cuenta: ¡no hay nada especial en -100 y 100! Si empiezas con un número entre -1000 y 1000, sabes que acabarás adivinando el número correcto aunque te cueste unas cuantas veces más. Te diriges a tu segunda clase victorioso, confiado en que estarás preparado para el siguiente reto de Jordan.
Convertir fracción mixta a decimal
Convertir cualquier decimal final en una fracción es bastante sencillo. Se cuenta el número de decimales, se mueve el punto decimal ese número de lugares a la derecha, y se pone el número resultante sobre el “1” seguido de ese número de ceros.
El decimal tenía dos posiciones decimales, así que moví el punto dos unidades a la derecha, y luego puse el número resultante (es decir, “46”) sobre “1” seguido de dos ceros (también conocido como “100”). Luego simplifiqué.
Este decimal también tenía un solo decimal, así que el proceso cuando el mismo que antes. Está bien tener varios dígitos a la izquierda del punto decimal en la forma decimal original. Simplemente, acabarás con una fracción impropia más grande cuando termines de convertirla.
Este decimal tenía cuatro posiciones decimales, aunque sólo un dígito de interés (el “3”). Moví el punto cuatro lugares a la derecha, y puse el número resultante sobre “1” seguido de cuatro ceros (también conocido como “10.000”). La fracción resultante no se simplificó en absoluto.