Cual es el area de un circulo
Contenidos
Cómo encontrar el radio de un círculo
Vamos a hacer un recorrido por la información más esencial sobre el área de un círculo, su diámetro y su radio. Aprenderemos a encontrar el área de un círculo, hablaremos de la fórmula del área de un círculo y discutiremos las otras ramas de las matemáticas que utilizan la misma ecuación.¿Cómo calcular el área de un círculo? Fórmula del área del círculo
El área de un círculo hallada con las calculadoras de radio y diámetro sirve de base para muchas otras ecuaciones, no sólo en matemáticas, sino también en la vida cotidiana. He aquí algunos ejemplos en los que puede ser útil saber cómo encontrar el área de un círculo:
Fórmula de la superficie de un círculo
Soluciones[ \textbf{diámetro} \, d = 2r \]\[d = 2 \times 12 \]\[d = 24 \]\[\textbf{circunferencia} \, C = 2 \pi r \]\[C = 2 \pi \times 12 \]\[C = 24 \pi \]\[C = 75. 3982237 \N – A = \pi r^2 \N – [A = \pi \N – 12^2 \N – [A = 144 \pi \N – [A = 452.389342 \N -]
Unidades: Tenga en cuenta que las unidades de longitud se muestran por conveniencia. No afectan a los cálculos. Las unidades están para dar una indicación del orden de los resultados, como pies, pies2 o pies3. Se puede sustituir por cualquier otra unidad base.
Perímetro de un círculo
Explicación: Como se dice que A es el centro del círculo y ABCD es un cuadrado, el ángulo BAD es un ángulo recto que comprende exactamente la cuarta parte del círculo (90o es la cuarta parte de 360o). Esto también puede verse a través de una proporción.
Como el ángulo que contiene el área roja es una cuarta parte del círculo, encontrar el área de todo el círculo, y luego una cuarta parte de ese número da la respuesta. Usa la ecuación para encontrar el área de un círculo, donde es el área y es el radio.
Explicación: Para hallar el área de toda la pista, halla el área del rectángulo en el centro de la pista y súmala al área del círculo que formarían los dos semicírculos en los bordes de ese rectángulo.
Explicación: Utilizando el Teorema de Pitágoras, se puede encontrar que el diámetro del círculo (también la diagonal del cuadrado) es 4√2. Por tanto, el radio del círculo es la mitad del diámetro, es decir, 2√2. El área del círculo es entonces π(2√2)2, que es igual a 8π. A continuación, hay que restar el área del cuadrado a todo el círculo, lo que da como resultado un área de 8π-16 pulgadas cuadradas.
Cómo encontrar el área de un círculo con el radio
En geometría, el área encerrada por un círculo de radio r es πr2. En este caso, la letra griega π representa la relación constante entre la circunferencia de cualquier círculo y su diámetro, aproximadamente igual a 3,1416.
Un método para derivar esta fórmula, que tiene su origen en Arquímedes, consiste en considerar el círculo como el límite de una secuencia de polígonos regulares. El área de un polígono regular es la mitad de su perímetro multiplicado por la distancia de su centro a sus lados, y la fórmula correspondiente -que el área es la mitad del perímetro por el radio-, es decir, A = 1/2 × 2πr × r, se cumple en el límite para un círculo.
Aunque en contextos informales se suele hablar del área de un círculo, en sentido estricto el término disco se refiere al interior del círculo, mientras que el círculo se reserva sólo para el límite, que es una curva y no cubre ninguna superficie en sí. Por lo tanto, el área de un disco es la frase más precisa para el área encerrada por un círculo.
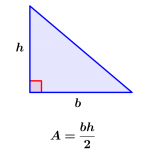
Las matemáticas modernas pueden obtener el área utilizando los métodos del cálculo integral o de su descendiente más sofisticado, el análisis real. Sin embargo, el área de un disco fue estudiada por los antiguos griegos. Eudoxo de Cnidus, en el siglo V a.C., descubrió que el área de un disco es proporcional a su radio al cuadrado[1]. Arquímedes utilizó las herramientas de la geometría euclidiana para demostrar que el área dentro de un círculo es igual a la de un triángulo rectángulo cuya base tiene la longitud de la circunferencia del círculo y cuya altura es igual al radio del círculo en su libro Medición de un círculo. La circunferencia es 2πr, y el área de un triángulo es la mitad de la base por la altura, lo que da como resultado el área π r2 del disco. Antes de Arquímedes, Hipócrates de Quíos fue el primero en demostrar que el área de un disco es proporcional al cuadrado de su diámetro, como parte de su cuadratura de la luna de Hipócrates,[2] pero no hizo n