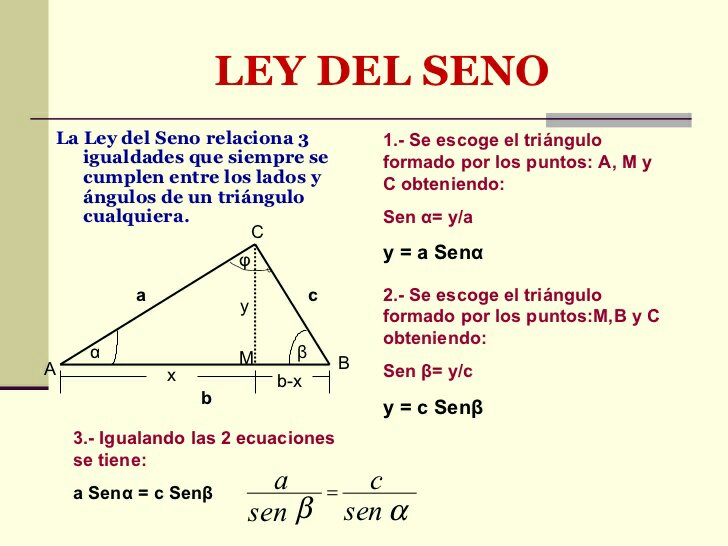
Formula seno y coseno
Contenidos
Formula seno y coseno online
Si se dan dos lados y un ángulo interior de un triángulo, y el lado opuesto al ángulo dado es el más corto de los dos lados, entonces podemos dibujar dos triángulos diferentes (\(\triangle NMP\) y \(\triangle NMP’\)), ambos con las dimensiones dadas. Llamamos a este caso ambiguo porque hay dos formas de interpretar la información dada y no es seguro cuál es la solución requerida.
Observamos que para las dimensiones dadas del triángulo ABC, el lado BC opuesto a A es más corto que AB. Esto significa que podemos dibujar dos triángulos diferentes con las dimensiones dadas.
Hay una costa con dos faros, uno a cada lado de una playa. Los dos faros están separados por una distancia de \(\text{0,67}) \(\text{km}) y uno está exactamente al este del otro. Los faros indican la proximidad de una embarcación tomando rumbos hacia ella (un rumbo es un ángulo medido en el sentido de las agujas del reloj desde el norte). Estas orientaciones se muestran en el siguiente diagrama.
Vemos que los dos faros y el barco forman un triángulo. Como sabemos la distancia entre los faros y tenemos dos ángulos, podemos utilizar la trigonometría para encontrar los dos lados restantes del triángulo, la distancia del barco a los dos faros.
Valores exactos del seno y el coseno: regla del coseno y área 1
Has visto bastantes identidades trigonométricas en las últimas páginas. Es conveniente tener un resumen de ellas como referencia. Estas identidades se refieren en su mayoría a un ángulo denotado θ, pero hay algunas que implican dos ángulos, y para ellas, los dos ángulos se denotan α y β.
Además: curiosamente, estas identidades de producto se utilizaban antes de que se inventaran los logaritmos para realizar la multiplicación. Así es como se puede utilizar la segunda. Si quieres multiplicar x por y, utiliza una tabla para buscar el ángulo α cuyo coseno es x y el ángulo β cuyo coseno es y. Busca los cosenos de la suma α + β. y de la diferencia α – β. Haz la media de esos dos cosenos. ¡Obtienes el producto xy! Tres búsquedas en la tabla, y el cálculo de una suma, una diferencia y un promedio en lugar de una multiplicación. Tycho Brahe (1546-1601), entre otros, utilizó este algoritmo conocido como prosthaphaeresis.
Regla del seno y del coseno 1 (gcse higher maths)- tutorial 17
En matemáticas, las identidades trigonométricas son igualdades que implican funciones trigonométricas y son verdaderas para cada valor de las variables que ocurren para las que se definen ambos lados de la igualdad. Geométricamente, son identidades que implican ciertas funciones de uno o más ángulos. Son distintas de las identidades de los triángulos, que son identidades que implican potencialmente a los ángulos pero también a las longitudes de los lados u otras longitudes de un triángulo.
Estas identidades son útiles cuando hay que simplificar expresiones que implican funciones trigonométricas. Una aplicación importante es la integración de funciones no trigonométricas: una técnica común consiste en utilizar primero la regla de sustitución con una función trigonométrica y luego simplificar la integral resultante con una identidad trigonométrica.
Signos de las funciones trigonométricas en cada cuadrante. La mnemotecnia “Todos los profesores de ciencias (están) locos” enumera las funciones básicas (‘Todos’, sen, tan, cos) que son positivas de los cuadrantes I a IV.[1] Se trata de una variación de la mnemotecnia “Todos los estudiantes hacen cálculo”.
9-1 gcse maths – regla del seno y del coseno – cuál usar
Bueno, en cálculo usamos MUCHO las funciones trigonométricas: en sustituciones integrales, en series, series de taylor (como las que mostré ahora), derivadas, pruebas de convergencia (como la onde de Euler en el problema de basel) y otras cosas…
Todas las definiciones que veo, son un poco circulares o no lo suficientemente rigurosas para hacerme sentir bien tomando algunas derivadas o sustituciones integrales, porque siempre me importa el dominio de estas cosas. Así que quiero definirlo muy bien y poder usar todas las identidades trigonométricas.
ps: Sé que usé algunas palabras primitivas en algunas definiciones, como ‘viaje’, así que las dejé en el énfasis, pero espero que ustedes entiendan. Y perdón por el largo post, pero necesitaba hacerlo, porque nunca he visto una definición completa en ningún libro. Gracias.
La definición estándar de las funciones trigonométricas es en términos de un círculo unitario. La definición clásica en términos de triángulos rectos es más limitada en cuanto a su alcance. Por ello, en el Cálculo se utiliza la definición más robusta en términos de la circunferencia unitaria. A partir de esta definición “estándar” se pueden demostrar todas las identidades de las funciones trigonométricas.