Como sacar porcentajes de cantidades

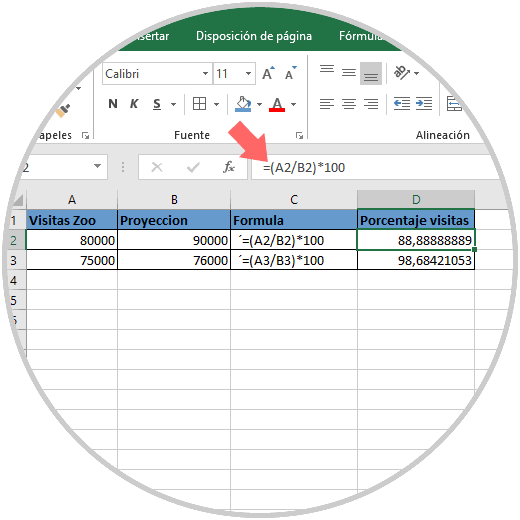
Calculadora de porcentajes

En matemáticas, un porcentaje (del latín per centum “por cien”) es un número o ratio expresado como una fracción de 100. A menudo se denota con el signo de porcentaje, “%”,[1][2] aunque también se utilizan las abreviaturas “pct.”, “pct” y a veces “pc”.[3] Un porcentaje es un número adimensional (número puro); no tiene unidad de medida.
Aunque muchos valores porcentuales se sitúan entre 0 y 100, no existe ninguna restricción matemática y los porcentajes pueden adoptar otros valores[4]. Por ejemplo, es habitual referirse al 111% o al -35%, especialmente en el caso de cambios y comparaciones porcentuales.
En la antigua Roma, mucho antes de que existiera el sistema decimal, los cálculos se hacían a menudo en fracciones en los múltiplos de 1/100. Por ejemplo, Augusto imponía un impuesto de 1/100 sobre los bienes vendidos en subasta, conocido como centesima rerum venalium. El cómputo con estas fracciones era equivalente al de los porcentajes.
A medida que las denominaciones del dinero crecían en la Edad Media, los cálculos con un denominador de 100 se hicieron cada vez más habituales, de manera que desde finales del siglo XV hasta principios del XVI, se hizo común que los textos de aritmética incluyeran tales cálculos. Muchos de estos textos aplicaban estos métodos a las pérdidas y ganancias, los tipos de interés y la regla de tres. En el siglo XVII, era habitual citar los tipos de interés en centésimas[5].

Fórmula porcentual

El objetivo de esta serie de lecciones es sintetizar los conocimientos de los alumnos sobre el valor de las fracciones y los decimales para que puedan trabajar con porcentajes, con comprensión y competencia. Se hace un gran uso de materiales concretos para consolidar la comprensión de los alumnos.
La capacidad de comprender y trabajar de forma competente con los porcentajes depende de que los alumnos tengan una sólida comprensión del valor posicional, de nuestro sistema numérico decimal y de las fracciones y sus operaciones. Es importante que los alumnos tengan la oportunidad de explorar, reconocer, demostrar y articular estas conexiones por sí mismos, y que sean capaces de trabajar con fluidez entre ellas.
El pensamiento relacional sustenta la capacidad del alumno para comprender que un porcentaje se utiliza para expresar lo grande o pequeña que es una cantidad en relación con otra (que es mayor que cero). Un porcentaje es una relación entre una parte y un todo.
Un porcentaje es una forma de expresar una fracción de 100, u otra forma de escribir centésimas. Porcentaje, del latín per centum, significa literalmente de (por) cien (cent). El símbolo % está formado por el signo / por y los dos ceros (00) del número 100. Es importante utilizar una serie de representaciones físicas para garantizar que los alumnos puedan ver claramente y establecer las conexiones entre la fracción: por ejemplo, 75/100 (o 3/4), porcentaje 75% y representación decimal 0,75 de la misma cantidad.

Aerle.es

Porcentaje de una fórmula de cantidad

Los porcentajes se utilizan ampliamente y en muchos ámbitos diferentes. Por ejemplo, los descuentos en las tiendas, los tipos de interés bancarios, las tasas de inflación y muchas estadísticas de los medios de comunicación se expresan en porcentajes. Los porcentajes son importantes para comprender los aspectos financieros de la vida cotidiana.
Los porcentajes son una forma útil de comparar fracciones con diferentes denominadores. Los porcentajes proporcionan información que suele ser más fácil de entender que las fracciones. Por ejemplo, una afirmación como “el 60% de la población tiene el pelo castaño” es bastante difícil de interpretar, mientras que la afirmación “el 60% de la población tiene el pelo castaño” es más fácil de entender ( ≈ 59%).
Los porcentajes se utilizan a menudo para comparar relaciones (fracciones) expresándolas como porcentajes. Por ejemplo, en dos exámenes un alumno obtiene 72 de 85 y 37 de 45. Expresando estos resultados como porcentajes se obtiene el 84,7% y el 82,2%, donde los porcentajes se dan correctos con un decimal. Por tanto, el primer resultado es mejor.
Dos panaderías llamadas Browie y Best Bake elaboran pan. En un día concreto, 27 de los 40 panes de la panadería Browie se habían horneado el día anterior. En la panadería Best Bake, 57 de los 90 panes se habían horneado el día anterior. ¿Qué panadería vendía el mayor porcentaje de panes horneados el día anterior?

Cómo hallar el porcentaje de algo

Aparte de los cálculos aritméticos básicos como la suma y la multiplicación, el cálculo de porcentajes de cantidades es uno de los cálculos más comunes que se realizan en la vida real. Algunos ejemplos cotidianos son:
Cuando la biomasa (por ejemplo, alimentos, plásticos y residuos agrícolas) se calienta rápidamente a 500º centígrados durante unos minutos en ausencia de oxígeno (en un proceso llamado pirólisis), se obtiene un combustible similar al gasóleo. La masa de los residuos originales se reduce al 60% durante el proceso de calentamiento. Si se pirolizan 1.000 kg de residuos de granja de pavos (es decir, plumas y excrementos), ¿cuál es la masa de biocombustible que se obtiene?