Potencia de potencias
Contenidos
Regla del exponente negativo
Gráficas de y = bx para varias bases b: base 10, base e, base 2, base 1/2. Cada curva pasa por el punto (0, 1) porque cualquier número distinto de cero elevado a la potencia de 0 es 1. En x = 1, el valor de y es igual a la base porque cualquier número elevado a la potencia de 1 es el propio número.
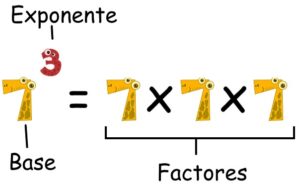
La exponenciación es una operación matemática, escrita como bn, que involucra dos números, la base b y el exponente o potencia n, y se pronuncia como “b elevado a la potencia de n”.[1][2] Cuando n es un entero positivo, la exponenciación corresponde a la multiplicación repetida de la base: es decir, bn es el producto de multiplicar n bases:[2]
El exponente suele aparecer como un superíndice a la derecha de la base. En ese caso, bn se llama “b elevado a la enésima potencia”, “b elevado a la potencia de n”,[1] “la enésima potencia de b”, “b a la enésima potencia”,[3] o más brevemente como “b a la enésima”.
Se tiene b1 = b, y, para cualesquiera enteros positivos m y n, se tiene bn ⋅ bm = bn+m. Para extender esta propiedad a exponentes enteros no positivos, se define b0 como 1, y b-n (con n un entero positivo y b no cero) como 1/bn. En particular, b-1 es igual a 1/b, el recíproco de b.
Exponentes negativos
La propiedad del cociente (propiedad del cociente de potencias, regla del cociente de potencias) establece que podemos dividir dos potencias con la misma base simplemente restando sus exponentes y conservando su base común. Por ejemplo, al dividir la expresión algebraica y18 entre y12 obtendremos un resultado igual a y18-12, o y6, donde y puede representar cualquier valor numérico excepto 0; recordemos que la Propiedad del Cociente sólo es aplicable si las expresiones comparten una base común y esa base no debe ser igual a cero. La base no puede ser cero porque no está definida por las propiedades de la aritmética: si 12 pudiera dividirse por 0, por ejemplo, esto significaría que la ecuación 0 por y = 12 tendría solución… ¡lo cual no es posible!
La propiedad del cociente funciona porque si lo hacemos de la manera “larga” expandiendo cada expresión, y18 = y-y-y-y-y-y-y-y-y-y-y-y y12 = y-y-y-y-y-y-y-y-y-y-y-y, y luego dividimos, podemos ver que las 12 y’s del denominador se cancelarán con 12 de las y’s del numerador, dejando sólo 6 “y’s” restantes en el numerador y ninguna y’s (o el número 1) en el denominador.
Definición del poder de los poderes
Creo que aquí me decantaría por “poderes”, simplemente porque contrasta los poderes de un rey con los “poderes enumerados” que figuran en la Constitución de Estados Unidos. Sin embargo, se podría hacer un caso similar con el término “poder ejecutivo”.
Tanto “poderes enumerados” como “poder(es) ejecutivo(s)” son términos comunes en la ciencia política para describir (entre otras cosas) los poderes del gobierno. También son comunes muchos otros términos que contienen “poder”; el problema es que la mayoría de ellos pueden usarse tanto en singular como en plural.
En general, la diferencia entre “poder” y “poderes” es sutil. El “poder” suele utilizarse de forma más amplia y general para describir las acciones o el control que puede ejercer un grupo o un individuo. En cambio, “poderes” suele utilizarse para referirse a un conjunto de capacidades específicas y bien definidas de un grupo o individuo. Todo depende de lo que se entienda por “poder(es)”.
Podrías sustituirlo, pero sonaría incómodo porque no encaja con el contexto de la frase. Normalmente, cuando alguien afirma que no tiene poder en el gobierno, está hablando del aspecto general del poder, no de poderes separados y distintos.
Comentarios
Anime a los alumnos de un grupo de enseñanza guiada a decir “he movido el 1 a lo largo de 8 lugares” en lugar de “he añadido 8 ceros” cuando estén prediciendo lo que sería 108. La regla “añadir un cero” para multiplicar por 10 es conceptualmente inexacta. Matemáticamente, añadir un 0 a un número no lo cambia: 12 + 0 = 12. Esta “regla” también prepara a los alumnos para que tengan problemas más adelante cuando multipliquen fracciones decimales porque 5,6 x 10 no es igual a 5,60. Es mejor que los alumnos aprendan a entender principios matemáticos que siempre son verdaderos que aprender muchas reglas que hay que cambiar continuamente en diferentes situaciones.
La generalización en este caso es que cuando multiplicamos por 10, los números se desplazan un lugar a la izquierda; son los dígitos los que se mueven, no la coma decimal. Puedes demostrarlo escribiendo el número 43 en una tira de papel debajo de las casas de valor posicional y desplazando la tira 1 lugar hacia la izquierda para multiplicar por 10. Esto crea un espacio bajo la columna de las unidades, donde hay que escribir un 0 como “marcador de posición” porque si no tuviéramos las etiquetas de las casas sobre los números, no sabríamos si el número debería ser 43 o 430. Es importante utilizar el valor posicional