Razon trigonometrica seno
Contenidos
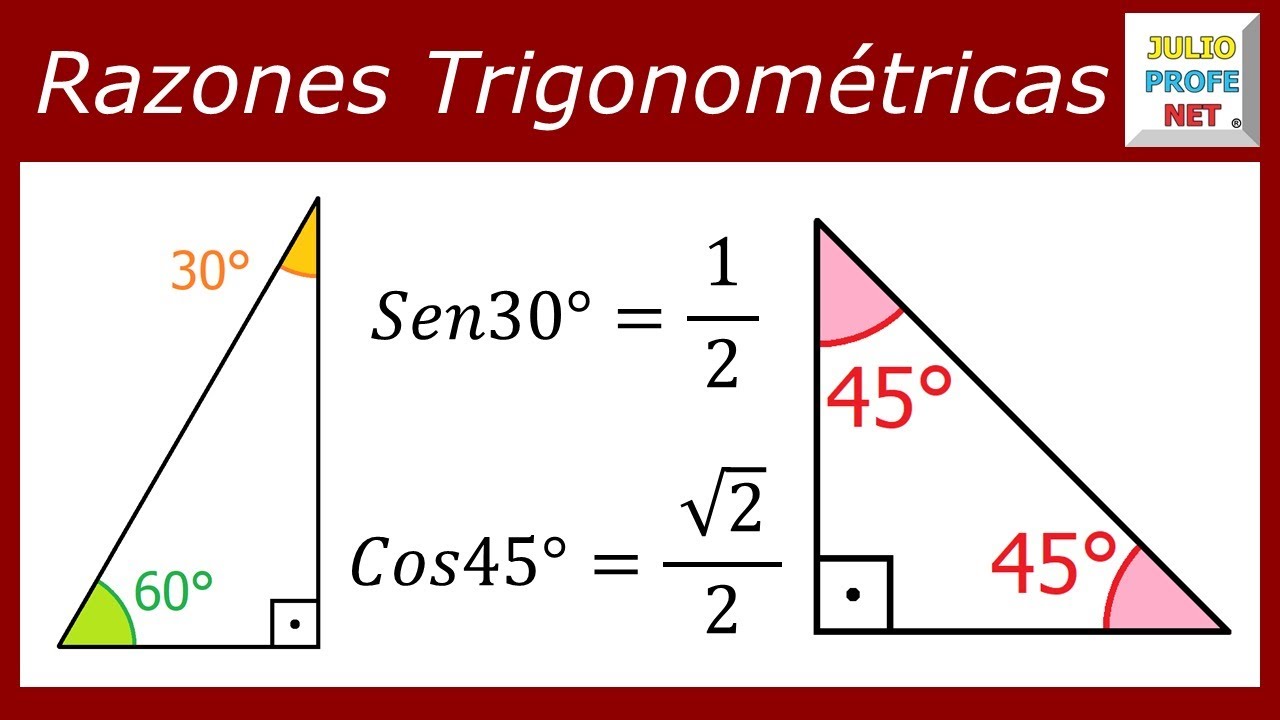
Razones trigonométricas
¿Sabes lo que se dicen dos ángulos que viven dentro del mismo triángulo rectángulo? El primer ángulo dice: “Oye Thelma (¿o es Theta?), no quiero salirme por la tangente, pero ¿cuál es tu seno?”. A lo que el segundo ángulo responde: “Phil (¿o es Phi?), no sé por qué te molestas en preguntar, ¡mi seno es obviamente el mismo que tu coseno!”.
Vale, quizá no sea el mejor chiste del mundo, pero una vez que entiendes los senos y los cosenos, es bastante divertido. Por supuesto, eso significa que si no conoces la diferencia entre un seno y un coseno, actualmente te has quedado fuera en el frío metafórico.
Cuando hablamos del mundo de la trigonometría, aprendimos que la parte de las matemáticas llamada trigonometría se ocupa de los triángulos. Y, en particular, es la parte de las matemáticas que se ocupa de averiguar la relación entre los tres lados y los tres ángulos que componen cada triángulo.
Nos interesa especialmente el tipo especial de triángulos conocido como triángulos rectángulos. Todos los triángulos rectángulos tienen un ángulo de 90 grados (como la esquina de un cuadrado o un rectángulo) y dos ángulos que oscilan entre 0 grados y 90 grados (como veremos más adelante, la suma de los tres ángulos es de 180 grados).
Tangente
Este artículo necesita citas adicionales para su verificación. Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables. El material sin fuente puede ser cuestionado y eliminado.Buscar fuentes: “Usos de la trigonometría” – noticias – periódicos – libros – scholar – JSTOR (marzo de 2012) (Aprende cómo y cuándo eliminar este mensaje de la plantilla)
El manipulador robótico Canadarm2 de la Estación Espacial Internacional se maneja controlando los ángulos de sus articulaciones. El cálculo de la posición final del astronauta en el extremo del brazo requiere el uso repetido de funciones trigonométricas de esos ángulos.
La trigonometría es conocida, sobre todo, por su aplicación a los problemas de medición entre el público no matemático y no científico, pero también se utiliza a menudo de forma mucho más sutil, como en la teoría de la música; otros usos son más técnicos, como en la teoría de los números. Los temas matemáticos de las series de Fourier y las transformadas de Fourier se basan en gran medida en el conocimiento de las funciones trigonométricas y tienen aplicación en diversos ámbitos, como la estadística.
Breve historia de la trigonometría
Divine Proportions: De la trigonometría racional a la geometría universal es un libro de 2005 del matemático Norman J. Wildberger sobre una propuesta de enfoque alternativo a la geometría y la trigonometría euclidianas. El libro aboga por sustituir las magnitudes básicas habituales de la trigonometría, la distancia euclidiana y la medida del ángulo, por la distancia al cuadrado y el cuadrado del seno del ángulo, respectivamente. Esto es lógicamente equivalente al desarrollo estándar (ya que las cantidades de sustitución pueden expresarse en términos de las estándar y viceversa), pero el autor afirma que su enfoque tiene algunas ventajas.
El libro fue “esencialmente autopublicado”[1] por Wildberger a través de su editorial Wild Egg. Las fórmulas y teoremas del libro se consideran matemáticas correctas, pero las afirmaciones sobre la superioridad práctica o pedagógica son promovidas principalmente por el propio Wildberger y han recibido críticas mixtas.
La idea principal de Divine Proportions es sustituir las distancias por la distancia euclidiana al cuadrado, rebautizada en este libro como “cuadrangular”, y sustituir los ángulos por los cuadrados de sus senos, rebautizados en este libro como “dispersión” y considerados como una medida de separación (más que una cantidad de rotación) entre dos líneas. Divine Proportions define ambos conceptos directamente a partir de las coordenadas cartesianas de los puntos que determinan un segmento de línea o un par de líneas que se cruzan, en lugar de hacerlo indirectamente a partir de las distancias y los ángulos. Definidas así, son funciones racionales de esas coordenadas, y pueden calcularse directamente sin necesidad de las raíces cuadradas necesarias para calcular distancias a partir de coordenadas o de las funciones trigonométricas inversas necesarias para calcular ángulos para coordenadas[1].
Identidades trigonométricas
Los primeros estudios sobre los triángulos se remontan al segundo milenio antes de Cristo, en las matemáticas egipcias (Papiro Matemático Rhind) y babilónicas. La trigonometría también estaba presente en las matemáticas kushitas[1].
El estudio sistemático de las funciones trigonométricas comenzó en las matemáticas helenísticas y llegó a la India como parte de la astronomía helenística[2] En la astronomía india, el estudio de las funciones trigonométricas floreció en el periodo Gupta, especialmente gracias a Aryabhata (siglo VI de nuestra era), que descubrió la función seno. Durante la Edad Media, el estudio de la trigonometría continuó en las matemáticas islámicas, de la mano de matemáticos como Al-Khwarizmi y Abu al-Wafa. Se convirtió en una disciplina independiente en el mundo islámico, donde se conocían las seis funciones trigonométricas. Las traducciones de textos árabes y griegos hicieron que la trigonometría se adoptara como materia en el Occidente latino a partir del Renacimiento con Regiomontanus. El desarrollo de la trigonometría moderna se produjo durante el Siglo de las Luces occidental, comenzando con las matemáticas del siglo XVII (Isaac Newton y James Stirling) y alcanzando su forma moderna con Leonhard Euler (1748).