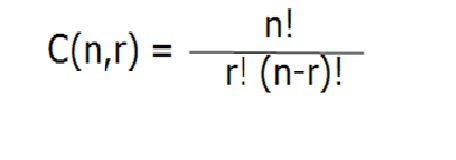Formula de combinacion
Contenidos
Formula de combinacion 2021
Las permutaciones y combinaciones se utilizan en las clases de matemáticas y en la vida cotidiana. Afortunadamente, son fáciles de calcular una vez que se sabe cómo hacerlo. A diferencia de las permutaciones, en las que el orden de los grupos es importante, en las combinaciones el orden no importa[1].
Las combinaciones te indican cuántas formas hay de combinar un número determinado de elementos de un grupo. Para calcular las combinaciones, sólo tienes que saber el número de elementos entre los que vas a elegir, el número de elementos a elegir y si se permite o no la repetición (en la forma más común de este problema, no se permite la repetición).
Formula de combinacion online
En matemáticas, una combinación es una selección de elementos de una colección, de manera que el orden de selección no importa (a diferencia de las permutaciones). Por ejemplo, dadas tres frutas, digamos una manzana, una naranja y una pera, hay tres combinaciones de dos que pueden extraerse de este conjunto: una manzana y una pera; una manzana y una naranja; o una pera y una naranja.
Las combinaciones se refieren a la combinación de n cosas tomadas k a la vez sin repetición. Para referirse a las combinaciones en las que se permite la repetición, se suelen utilizar los términos k-selección,[1] k-multiset,[2] o k-combinación con repetición[3] Si, en el ejemplo anterior, fuera posible tener dos de cualquier tipo de fruta, habría otras 3 2-selecciones: una con dos manzanas, otra con dos naranjas y otra con dos peras.
Aunque el conjunto de tres frutas era lo suficientemente pequeño como para escribir una lista completa de combinaciones, esto se vuelve poco práctico a medida que aumenta el tamaño del conjunto. Por ejemplo, una mano de póquer puede describirse como una combinación de 5 cartas (k = 5) de una baraja de 52 cartas (n = 52). Las 5 cartas de la mano son todas distintas, y el orden de las cartas en la mano no importa. Hay 2.598.960 combinaciones de este tipo, y la probabilidad de sacar una mano cualquiera al azar es de 1 / 2.598.960.
Formula de combinacion 2020
¿Alguien puede explicar por qué tenemos que dividir por el “número de maneras de reordenar las ranuras” para deshacernos de los duplicados? Entiendo que funciona y que la división se utiliza para reducir un número, pero no consigo ese “momento aha” de por qué lo hacemos. ¿Alguien puede explicarlo?
Por cada mano de tres cartas que puedas sacar, puedes sacar las mismas tres cartas en seis ordenes diferentes. Por lo tanto, al dividir por 6$, cada ordenamiento específico de tres cartas se reduce a un único conjunto de esas tres cartas.
Formula de combinacion del momento
En matemáticas, una combinación es una selección de elementos de una colección, de manera que el orden de selección no importa (a diferencia de las permutaciones). Por ejemplo, dadas tres frutas, digamos una manzana, una naranja y una pera, hay tres combinaciones de dos que pueden extraerse de este conjunto: una manzana y una pera; una manzana y una naranja; o una pera y una naranja.
Las combinaciones se refieren a la combinación de n cosas tomadas k a la vez sin repetición. Para referirse a las combinaciones en las que se permite la repetición, se suelen utilizar los términos k-selección,[1] k-multiset,[2] o k-combinación con repetición[3] Si, en el ejemplo anterior, fuera posible tener dos de cualquier tipo de fruta, habría otras 3 2-selecciones: una con dos manzanas, otra con dos naranjas y otra con dos peras.
Aunque el conjunto de tres frutas era lo suficientemente pequeño como para escribir una lista completa de combinaciones, esto se vuelve poco práctico a medida que aumenta el tamaño del conjunto. Por ejemplo, una mano de póquer puede describirse como una combinación de 5 cartas (k = 5) de una baraja de 52 cartas (n = 52). Las 5 cartas de la mano son todas distintas, y el orden de las cartas en la mano no importa. Hay 2.598.960 combinaciones de este tipo, y la probabilidad de sacar una mano cualquiera al azar es de 1 / 2.598.960.