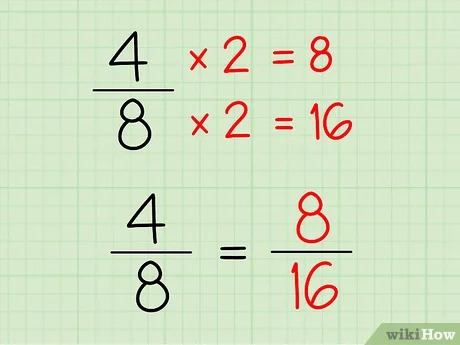Como se saca la equivalencia de una fraccion
Contenidos
Calculadora de fracciones equivalentes
Esta tarea está relacionada con un aspecto de 4.NF3.c, a saber, la escritura de un número mixto como fracción equivalente; otras tareas ilustran otros aspectos de este estándar. El propósito de esta tarea es ayudar a los alumnos a comprender y articular las razones de los pasos del algoritmo habitual para convertir un número mixto en una fracción equivalente, es decir
El segundo paso muestra que el algoritmo es simplemente un atajo para encontrar un denominador común entre dos fracciones. Este concepto es un precursor importante de la adición de números mixtos y fracciones con denominadores semejantes y, como tal, el paso dos debe ser un punto de énfasis.
Esta tarea es apropiada tanto para la enseñanza como para la evaluación formativa, y encaja perfectamente con el PM 3, Construir argumentos viables y criticar el razonamiento de otros. Si el objetivo es conseguir que los alumnos expliquen los pasos utilizando imágenes, podría ser necesaria una mayor orientación.
Finalmente, en la tercera imagen podemos contar todos los tercios y ver que tenemos 21 de los 7 enteros y 1 más, para un total de 22 tercios. Así que nuestra respuesta final es $\frac{22}{3}$. Interpretando adecuadamente las imágenes, podemos dar sentido a los pasos 3 y 4 de Ben.
Fracción equivalente de 2/3
Fracciones equivalentes: Se define como las fracciones que tienen numeradores y denominadores diferentes pero el mismo valor. Podemos decir que 2/6, 3/9 y 4/12 son las fracciones equivalentes que tienen números diferentes pero la misma proporción. Para obtener una fracción equivalente, podemos multiplicar o dividir el numerador y el denominador con el mismo número. No hay que sumar ni restar para encontrar fracciones equivalentes.
Puedes consultar las soluciones NCERT para el capítulo 2 de matemáticas de la clase 7 sobre fracciones y decimales para una mejor comprensión de los conceptos. Hemos proporcionado información detallada sobre las fracciones equivalentes en este artículo, sigue leyendo para conocer su definición y ejemplos.
La fracción equivalente se define como la fracción que tiene diferente numerador y denominador pero que representa el mismo valor. Dos o más fracciones son equivalentes si son iguales a la misma fracción cuando se multiplican. Por ejemplo, la fracción equivalente de 1/2 es 2/4, 3/6, 4/8. Podemos decir que tienen el mismo valor independientemente de su numerador y denominador.
Fracciones equivalentes a 1/2
Este artículo ha sido redactado por David Jia. David Jia es un tutor académico y el fundador de LA Math Tutoring, una empresa de tutoría privada con sede en Los Ángeles, California. Con más de 10 años de experiencia en la enseñanza, David trabaja con estudiantes de todas las edades y grados en diversas materias, así como en el asesoramiento de admisión a la universidad y la preparación de exámenes para el SAT, ACT, ISEE, y más. Después de obtener una puntuación perfecta de 800 en matemáticas y 690 en inglés en el SAT, David fue galardonado con la beca Dickinson de la Universidad de Miami, donde se graduó con una licenciatura en Administración de Empresas. Además, David ha trabajado como instructor de videos en línea para compañías de libros de texto como Larson Texts, Big Ideas Learning y Big Ideas Math.
Dos fracciones son equivalentes si tienen el mismo valor. Saber cómo convertir una fracción en una equivalente es una habilidad matemática esencial que es necesaria para todo, desde el álgebra básica hasta el cálculo avanzado. Este artículo cubrirá varias maneras de calcular fracciones equivalentes, desde la multiplicación y división básicas hasta métodos más complejos para resolver ecuaciones de fracciones equivalentes.
Fracciones equivalentes a 1/3
La parte sombreada en la imagen (ii) está representada por la fracción \(\frac{2}{4}\). En la imagen (iii) la misma parte está representada por la fracción \(\frac{4}{8}\). Por lo tanto, la fracción representada por estas partes sombreadas son iguales. Decimos que \N(\frac{1}{2}}) = \N(\frac{2}{4}}) = \N(\frac{4}{8}})Por tanto, para una fracción dada puede haber muchas fracciones equivalentes. Haciendo fracciones equivalentes: Hemos visto en el ejemplo anterior que \(\frac{1}{2}}), \(\frac{2}{4}}) y \(\frac{4}{8}}) son fracciones equivalentes. Por lo tanto, \frac{1}{2}} puede escribirse como \frac{1}{2}} = \frac{1}{2}{2}}) = \frac{1}{2}{2}}) = \frac{1}{3}{2}{3}} = \frac{1}{4}{2}{4}} y así sucesivamente. Por lo tanto, se puede obtener una fracción equivalente de cualquier fracción dada multiplicando su numerador y denominador por el mismo número.De la misma manera, cuando el numerador y el denominador de una fracción se dividen por el mismo número, obtenemos sus fracciones equivalentes. \(\frac{1}{2}}) = \(\frac{1 ÷ 1}{2 ÷ 1}\) = \(\frac{2}{4}\) = \(\frac{2 ÷ 2}{4 ÷ 2}\) = \(\frac{3}{6}\) = \(\frac{3 ÷ 3}{6 ÷ 3}\) Tenemos,