Multiplicaciones de dos cifras abajo
Contenidos
Multiplicación de 2 dígitos por 1 dígito sin reagrupación
● Cuatro operaciones fundamentales – hojas de trabajoHoja de trabajo sobre la adición.Hoja de trabajo sobre problemas de palabras sobre la adición.Hoja de trabajo sobre la sustracción.Hoja de trabajo sobre la adición y sustracción mixta.Hoja de trabajo sobre problemas de palabras sobre la adición y sustracción.Hoja de trabajo por adición o sustracción.Hoja de trabajo sobre la estimación de sumas y diferencias.Hoja de trabajo sobre la multiplicación.Hoja de trabajo sobre la multiplicación de un número por otro de 2 cifras. Hoja de trabajo sobre la multiplicación de un número por un número de tres cifras.Hoja de trabajo sobre la estimación de productos.Hoja de trabajo sobre problemas de palabras sobre la multiplicación.Hoja de trabajo sobre la división.Hoja de trabajo sobre los hechos de la división.Hoja de trabajo sobre la estimación del cociente.Hoja de trabajo sobre la división de números.Hoja de trabajo sobre la división por números de dos cifras.Hoja de trabajo sobre problemas de palabras sobre la división.Hoja de trabajo sobre cuatro operaciones fundamentales.Hoja de trabajo sobre sistemas de numeración.
Truco para multiplicar números de 2 cifras
La multiplicación de dos dígitos es simplemente una multiplicación de un solo dígito realizada dos veces. Comienza de la misma manera, multiplicando los números en el lugar de las unidades, y luego se añade una segunda ronda de multiplicación utilizando los números del lugar de las decenas. Después de aprender la fórmula básica, también hay algunos trucos que puedes dominar para que este proceso sea lo más rápido posible.
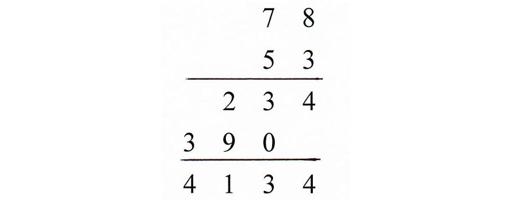
Resumen del artículoPara hacer una multiplicación de dos dígitos, empieza por poner un número encima del otro y dibuja una línea debajo de ellos. A continuación, multiplica el número inferior de unos por el número superior de unos y escribe la respuesta debajo de la línea. A continuación, multiplica el número inferior de las unidades por el número superior de las decenas y escribe la respuesta al lado de la primera respuesta. Una vez hecho esto, coloca un 0 debajo del resultado. Multiplica el número de las decenas de abajo por el número de las decenas de arriba y suma ambos resultados para obtener la respuesta final. Para aprender a llevar los resultados mayores que 9, desplázate hacia abajo.
Ejemplo de multiplicación de 2 dígitos por 1 dígito
Hemos hecho un poco de trampa introduciendo algunas multiplicaciones de dos y tres dígitos en nuestra sección de carga. Sin embargo, estábamos trabajando con números fáciles. Las reglas son fáciles si estás multiplicando un número de dos dígitos por un número de un dígito. Multiplica el valor de las unidades y luego multiplica el valor de las decenas.
Entonces, ¿qué ocurre si tienes dos números de dos cifras como factores? Aunque te llevará un poco más de tiempo, es un proceso fácil para resolver el problema. Sólo tienes que hacer dos problemas de multiplicación y luego sumar las respuestas. ¿Cómo puede ser tan sencillo? Veamos.
¿Crees que ya puedes sumar los dos valores? No. Hay un truco. Cuando multipliques la segunda parte, añade un “0” a esa respuesta, porque estás multiplicando el valor de la columna de las decenas (el 2). Si es de las decenas, añade un cero. Si es de las centenas, añade dos ceros.
Puede ser difícil de entender cuando se escribe esta idea con palabras, pero el concepto es sencillo. Si tu segundo factor (o el inferior) tiene dos dígitos, haces dos problemas de multiplicación. En la siguiente sección verás rápidamente que si tu segundo factor tiene tres dígitos, completarás tres problemas de multiplicación.
Multiplicación de 3 dígitos por 2 dígitos
Un algoritmo de multiplicación es un algoritmo (o método) para multiplicar dos números. Dependiendo del tamaño de los números, se utilizan diferentes algoritmos. Existen algoritmos de multiplicación eficientes desde la aparición del sistema decimal.
El método de la cuadrícula (o método de la caja) es un método introductorio para la multiplicación de varios dígitos que se suele enseñar a los alumnos de la escuela primaria o elemental. Ha sido una parte estándar del plan de estudios nacional de matemáticas de la escuela primaria en Inglaterra y Gales desde finales de la década de 1990[1].
Ambos factores se descomponen (“dividen”) en sus partes de centenas, decenas y unidades, y los productos de las partes se calculan entonces explícitamente en una etapa relativamente sencilla de sólo multiplicación, antes de que estas contribuciones se sumen para dar la respuesta final en una etapa separada de adición.
Este enfoque de cálculo (aunque no necesariamente con la disposición explícita de la cuadrícula) también se conoce como algoritmo de productos parciales. Su esencia es el cálculo de las multiplicaciones simples por separado, dejando toda la suma para la etapa final de reunión.