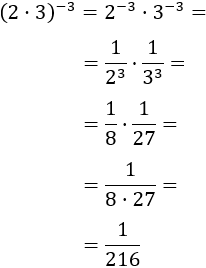Ejemplos de potencia de una potencia
Contenidos
Comentarios
Gráficas de y = bx para varias bases b: base 10, base e, base 2, base 1/2. Cada curva pasa por el punto (0, 1) porque cualquier número distinto de cero elevado a la potencia de 0 es 1. En x = 1, el valor de y es igual a la base porque cualquier número elevado a la potencia de 1 es el propio número.
La exponenciación es una operación matemática, escrita como bn, que implica dos números, la base b y el exponente o potencia n, y se pronuncia como “b elevado a la potencia de n”.[1][2] Cuando n es un número entero positivo, la exponenciación corresponde a la multiplicación repetida de la base: es decir, bn es el producto de multiplicar n bases:[2]
El exponente suele aparecer como un superíndice a la derecha de la base. En ese caso, bn se llama “b elevado a la enésima potencia”, “b elevado a la potencia de n”,[1] “la enésima potencia de b”, “b a la enésima potencia”,[3] o más brevemente como “b a la enésima”.
Se tiene b1 = b, y, para cualesquiera enteros positivos m y n, se tiene bn ⋅ bm = bn+m. Para extender esta propiedad a exponentes enteros no positivos, se define b0 como 1, y b-n (con n un entero positivo y b no cero) como 1/bn. En particular, b-1 es igual a 1/b, el recíproco de b.
Potencia de una ley de potencia ejemplos
cálculo de la FFT cuando la longitud de la señal no es una potencia exacta de 2.Examplescollapse allSiguiente potencia de 2 de valores enteros dobles Open Live ScriptDefina un vector de valores enteros dobles y calcule los exponentes para la siguiente potencia de 2 superior a esos valores. a = [1 -2 3 -4 5 9 519];
Siguiente potencia de 2 de valores enteros sin signo Abrir Live ScriptDefina un vector de valores enteros sin signo y calcule los exponentes para la siguiente potencia de 2 superior a esos valores. a = uint32([1020 4000 32700]);
Optimizar FFT con Padding Open Live ScriptUtiliza la función nextpow2 para aumentar el rendimiento de fft cuando la longitud de una señal no es una potencia de 2. Crea un vector 1-D que contenga 8191 valores de muestra. rng default;
32 63])Tipos de datos: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64Capacidades extendidasArrays altos Calcula con arrays que tienen más filas de las que caben en la memoria. Esta función es totalmente compatible con las matrices altas. Para
Acelerar el código ejecutándolo en una unidad de procesamiento gráfico (GPU) mediante Parallel Computing Toolbox™.Esta función es totalmente compatible con las matrices de la GPU. Para más información, consulte Ejecutar funciones de MATLAB en una GPU (Parallel Computing Toolbox).Arrays distribuidos
Definición de la potencia de una propiedad
Regla de la potencia (potencias a potencias): (am)n = amn, esto dice que para elevar una potencia a una potencia hay que multiplicar los exponentes. Hay otras reglas que acompañan a la regla de las potencias, como la regla del producto a las potencias y la regla del cociente a las potencias.
Regla del exponente negativo: , dice que los exponentes negativos en el numerador se trasladan al denominador y se convierten en exponentes positivos. Los exponentes negativos en el denominador se mueven al numerador y se convierten en exponentes positivos. Sólo se mueven los exponentes negativos.
Regla del cociente: , dice que para dividir dos exponentes con la misma base, se mantiene la base y se restan las potencias. Esto es similar a la reducción de fracciones; cuando restas las potencias pones la respuesta en el numerador o en el denominador dependiendo de dónde se encuentre la potencia mayor. Si la potencia mayor está en el denominador, pon la diferencia en el denominador y viceversa, esto ayudará a evitar exponentes negativos.
Ahora que hemos revisado las reglas para los exponentes, aquí están los pasos requeridos para simplificar expresiones exponenciales (nota que aplicamos las reglas en el mismo orden en que fueron escritas arriba):
Potencia de una calculadora de potencia
Otra palabra para exponente es potencia. Es probable que hayas visto o escuchado un ejemplo como [latex]3^5[/latex] puede ser descrito como [latex]3[/latex] elevado a la [latex]5[/latex] potencia. En esta sección ampliaremos nuestras capacidades con los exponentes. Aprenderemos qué hacer cuando un término con una potencia se eleva a otra potencia, y qué hacer cuando dos números o variables se multiplican y ambos se elevan a un exponente. También aprenderemos qué hacer cuando números o variables que se dividen se elevan a una potencia. Empezaremos por elevar potencias a potencias.
Simplifiquemos [latex]^4}(5^{2}\right)^{4}[/latex]. En este caso, la base es [latex]5^2[/latex] y el exponente es [latex]4[/latex], así que multiplicamos [latex]5^{2}[/latex] cuatro veces: [latex]\left(5^{2}\right)^{4}=5^{2}\cdot5^{2}\cdot5^{2}\cdot5^{2}=5^{8}[/latex] (usando la regla del producto-sumando los exponentes).
[latex]|left(5^{2}\right)^{4}[/latex] es una potencia de una potencia. Es la cuarta potencia de [latex]5[/latex] a la segunda potencia. Y vimos arriba que la respuesta es [latex]5^{8}[/latex]. Observa que el nuevo exponente es el mismo que el producto de los exponentes originales: [latex]2\cdot4=8[/latex].