Diferencia entre potencia y exponente
Contenidos
Diferencia de exponentes
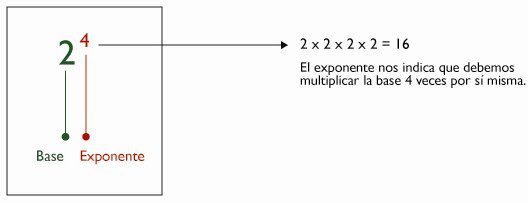
Respuesta) Conozcamos el exponente y la potencia.Una expresión que representa la multiplicación repetida de un mismo factor se conoce como potencia. Por ejemplo, 52 aquí, el número 5 se conoce como la base, y el número 2 se conoce como el exponente. El exponente es el 2 que corresponde al número de veces que se utiliza la base como factor.
Respuesta) La potencia (o el exponente) de un número define básicamente cuántas veces se utiliza el número en el proceso de multiplicación. Se escribe como un pequeño número a la derecha y encima del número base cuya potencia necesitamos encontrar.
Potencias y exponentes
Gráficas de y = bx para varias bases b: base 10, base e, base 2, base 1/2. Cada curva pasa por el punto (0, 1) porque cualquier número distinto de cero elevado a la potencia de 0 es 1. En x = 1, el valor de y es igual a la base porque cualquier número elevado a la potencia de 1 es el propio número.
La exponenciación es una operación matemática, escrita como bn, que implica dos números, la base b y el exponente o potencia n, y se pronuncia como “b elevado a la potencia de n”.[1][2] Cuando n es un número entero positivo, la exponenciación corresponde a la multiplicación repetida de la base: es decir, bn es el producto de multiplicar n bases:[2]
El exponente suele aparecer como un superíndice a la derecha de la base. En ese caso, bn se llama “b elevado a la enésima potencia”, “b elevado a la potencia de n”,[1] “la enésima potencia de b”, “b a la enésima potencia”,[3] o más brevemente como “b a la enésima”.
Se tiene b1 = b, y, para cualesquiera enteros positivos m y n, se tiene bn ⋅ bm = bn+m. Para extender esta propiedad a exponentes enteros no positivos, se define b0 como 1, y b-n (con n un entero positivo y b no cero) como 1/bn. En particular, b-1 es igual a 1/b, el recíproco de b.
Diferenciar el exponente de base y la potencia de un número
En matemáticas, te habrás fijado en el superíndice, es decir, un pequeño dígito que se coloca encima y a la derecha de cualquier número. Cuanto más grande es el número, más difícil es leerlo, compararlo y operar con él, por lo que los superíndices se utilizan para convertir los números más grandes en los más pequeños. Esto se hace con la ayuda de las potencias y los exponentes, que son el concepto básico de las matemáticas pero que también son yuxtapuestos por muchos estudiantes. Los exponentes representan el número de veces que se multiplica la base.
En matemáticas, el exponente implica el número pequeño, situado a la derecha del número base. Representa el número de veces que el número base se utiliza como factor, es decir, se multiplica por sí mismo. Pueden ser números, constantes e incluso variables. Cuando se utilizan exponentes para expresar un número grande, el proceso se denomina elevación a la potencia.
En las notaciones científicas, los exponentes son extremadamente importantes, ya que denotan cantidades grandes o pequeñas como potencias de 10. Por ejemplo, la distancia entre el Sol y la Tierra es de 1,496 × 1011 millones, la distancia entre el Sol y la Luna es de 3,84 × 108 millones. Hay ciertas reglas con respecto a los exponentes, que son:
Definir base y exponente
Regla de las potencias (Potencias a potencias): (am)n = amn, esto dice que para elevar una potencia a una potencia hay que multiplicar los exponentes. Hay otras reglas que acompañan a la regla de las potencias, como la regla del producto a las potencias y la regla del cociente a las potencias.
Regla del exponente negativo: , dice que los exponentes negativos en el numerador se trasladan al denominador y se convierten en exponentes positivos. Los exponentes negativos en el denominador se mueven al numerador y se convierten en exponentes positivos. Sólo se mueven los exponentes negativos.
Regla del cociente: , dice que para dividir dos exponentes con la misma base, se mantiene la base y se restan las potencias. Esto es similar a la reducción de fracciones; cuando restas las potencias pones la respuesta en el numerador o en el denominador dependiendo de dónde se encuentre la potencia mayor. Si la potencia mayor está en el denominador, pon la diferencia en el denominador y viceversa, esto ayudará a evitar exponentes negativos.
Ahora que hemos revisado las reglas para los exponentes, aquí están los pasos requeridos para simplificar expresiones exponenciales (nota que aplicamos las reglas en el mismo orden en que fueron escritas arriba):