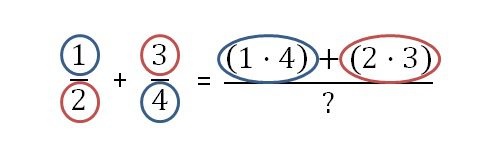Como sumar fraciones
Contenidos
Cómo multiplicar fracciones
Sumar fracciones con denominadores diferentes puede parecer complicado, pero una vez que los denominadores son iguales, la suma es muy fácil. Si trabajas con fracciones impropias en las que los numeradores son mayores que los denominadores, haz que los denominadores sean iguales. A continuación, suma los numeradores. Si estás sumando números mixtos, conviértelos en fracciones impropias y haz que cada fracción sea equivalente. Esto facilitará la suma de las fracciones.
Resumen del artículoPara sumar fracciones con denominadores diferentes, empieza por encontrar el mínimo común múltiplo de los denominadores. Luego, divide el mínimo común múltiplo entre el denominador de cada fracción. Toma el número que obtienes para cada fracción y multiplícalo por el numerador y el denominador de esa fracción, lo que hará que ambos denominadores sean iguales al mínimo común múltiplo. Por último, suma los numeradores y deja el denominador como está para obtener tu respuesta. Para saber cómo simplificar la respuesta, ¡sigue leyendo!
Cómo sumar fracciones con diferentes denominadores
Para tener éxito con esta lección, debes sentirte cómodo con la búsqueda del mínimo común múltiplo y la escritura de fracciones equivalentes. Por favor, vuelve a repasar estas lecciones si no dominas estas dos habilidades.
¿Necesita más ayuda con sus estudios de álgebra? ¡Obtenga acceso a cientos de ejemplos en video y problemas de práctica con su suscripción! Haga clic aquí para obtener más información sobre nuestras opciones de suscripción asequibles. Regístrese en nuestro curso gratuito de repaso de Pre-Álgebra.
Cómo renombrar fracciones
Este es el concepto básico de sumar fracciones con el mismo denominador. Las fracciones que tienen el mismo denominador también se llaman ‘Fracciones Similares’. Las fracciones que tienen diferentes denominadores se llaman “fracciones distintas”:
Si la respuesta resultante tiene el numerador mayor que el denominador, significa que la respuesta es una fracción impropia.Una fracción impropia es más de 1 entero por lo que debemos reescribirla como una fracción mixta o un número mixto.
Cuando se suman fracciones con los mismos denominadores, es similar a la idea de cortar algo en trozos más pequeños y luego sumar los trozos individuales.Cuando se trata de sumar fracciones con diferentes denominadores, nos encontramos con un problema. Cuando se trata de sumar fracciones con denominadores diferentes, nos encontramos con un problema: como los denominadores son diferentes, significa que cortamos el conjunto en tamaños diferentes:
En el diagrama podemos ver que el trozo de 1/3 y el trozo de 1/5 tienen tamaños diferentes. Si sumamos los dos trozos, ¿qué tamaño debería tener el resto de los trozos, el menor o el mayor? Así que cuando las fracciones tienen denominadores diferentes, tenemos que cambiar los denominadores para que sean iguales. Para ello, utilizamos fracciones equivalentes. La forma de conseguirlo es dividir cada trozo de la fracción de 1/3 en 5 trozos para obtener 5/15. Y dividir además cada trozo de 1/5 en 3 trozos para obtener 3/15 como se muestra a continuación:
Cómo dividir fracciones
Sumar fracciones es una habilidad muy útil. No sólo es una parte importante de la escuela -desde la primaria hasta la secundaria- sino que también es una habilidad muy práctica. Sigue leyendo para obtener más información sobre la suma de fracciones. En pocos minutos estarás dando vueltas al conocimiento.
Resumen del artículoPara sumar fracciones, empieza por comprobar el denominador de cada fracción para asegurarte de que es el mismo número. Si no es así, multiplica cada fracción por el denominador de la otra para darles un denominador común. Por ejemplo, al sumar ⅓ y ⅗, tu nuevo denominador sería 15, y las nuevas fracciones multiplicadas serían 5/15 y 9/15. Una vez que tengas el mismo denominador, suma sólo los numeradores y ponlos sobre el nuevo denominador. Para el ejemplo, la respuesta sería 14/15. Si quieres aprender a simplificar tus respuestas, ¡sigue leyendo el artículo!