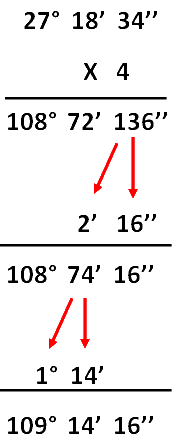
Como se realiza una multiplicacion

Cómo hacer el algoritmo de la multiplicación

¿Necesita seleccionar el nombre de cada registro (en nuestro caso, nombre) y calcular para él el resultado de multiplicar una columna numérica por otra (precio y cantidad)? Todo lo que tiene que hacer es utilizar el operador de multiplicación (*) entre las dos columnas del multiplicando (precio * cantidad) en una simple consulta SELECT. Puede dar a este resultado un alias con la palabra clave AS; en nuestro ejemplo, hemos dado a la columna de multiplicación un alias de precio_total.
Tenga en cuenta que también puede utilizar datos de dos columnas procedentes de tablas diferentes. Tenemos otra tabla en nuestra base de datos llamada discount que tiene columnas llamadas id y value; esta última representa el porcentaje de descuento en el artículo con el ID dado.
Como puede ver, es bastante fácil multiplicar valores de diferentes tablas unidas. En nuestro ejemplo anterior, hemos multiplicado el precio de cada producto por su cantidad desde una tabla (compra) y luego hemos multiplicado este precio total por el porcentaje de descuento utilizando la tabla de descuento.

Cómo hacer una multiplicación sin calculadora

La multiplicación compleja es una operación más difícil de entender tanto desde el punto de vista algebraico como geométrico. Hagámoslo primero algebraicamente, y tomemos unos números complejos concretos para multiplicar, digamos 3 + 2i y 1 + 4i. Cada uno tiene dos términos, así que cuando los multipliquemos, obtendremos cuatro términos:
Ahora el 12i + 2i se simplifica a 14i, por supuesto. ¿Y el 8i2? Recuerda que introdujimos i como abreviatura de √-1, la raíz cuadrada de -1. En otras palabras, i es algo cuyo cuadrado es -1. Así, 8i2 es igual a -8. Por tanto, el producto (3 + 2i)(1 + 4i) es igual a -5 + 14i.
Recuerda que (xu – yv), la parte real del producto, es el producto de las partes reales menos el producto de las partes imaginarias, pero (xv + yu), la parte imaginaria del producto, es la suma de los dos productos de una parte real y la otra imaginaria.
En otras palabras, sólo hay que multiplicar las dos partes del número complejo por el número real. Por ejemplo, 2 por 3 + i es simplemente 6 + 2i. Geométricamente, cuando se duplica un número complejo, sólo se duplica la distancia desde el origen, 0. De forma similar, cuando se multiplica un número complejo z por 1/2, el resultado estará a medio camino entre 0 y z. Se puede pensar en la multiplicación por 2 como una transformación que estira el plano complejo C en un factor de 2 lejos de 0; y la multiplicación por 1/2 como una transformación que aprieta C hacia 0.

Matematicas 3 primaria

Cómo multiplicar

Un algoritmo de multiplicación es un algoritmo (o método) para multiplicar dos números. Dependiendo del tamaño de los números, se utilizan diferentes algoritmos. Existen algoritmos de multiplicación eficientes desde la aparición del sistema decimal.
El método de la cuadrícula (o método de la caja) es un método introductorio para la multiplicación de varios dígitos que se suele enseñar a los alumnos de la escuela primaria o elemental. Ha sido una parte estándar del plan de estudios nacional de matemáticas de la escuela primaria en Inglaterra y Gales desde finales de la década de 1990[1].
Ambos factores se descomponen (“dividen”) en sus partes de centenas, decenas y unidades, y los productos de las partes se calculan entonces explícitamente en una etapa relativamente sencilla de sólo multiplicación, antes de que estas contribuciones se sumen para dar la respuesta final en una etapa separada de adición.
Este enfoque de cálculo (aunque no necesariamente con la disposición explícita de la cuadrícula) también se conoce como algoritmo de productos parciales. Su esencia es el cálculo de las multiplicaciones simples por separado, dejando toda la suma para la etapa final de reunión.

Cómo multiplicar rápidamente

Un algoritmo de multiplicación es un algoritmo (o método) para multiplicar dos números. Dependiendo del tamaño de los números, se utilizan diferentes algoritmos. Existen algoritmos de multiplicación eficientes desde la aparición del sistema decimal.
El método de la cuadrícula (o método de la caja) es un método introductorio para la multiplicación de varios dígitos que se suele enseñar a los alumnos de la escuela primaria o elemental. Ha sido una parte estándar del plan de estudios nacional de matemáticas de la escuela primaria en Inglaterra y Gales desde finales de la década de 1990[1].
Ambos factores se descomponen (“dividen”) en sus partes de centenas, decenas y unidades, y los productos de las partes se calculan entonces explícitamente en una etapa relativamente sencilla de sólo multiplicación, antes de que estas contribuciones se sumen para dar la respuesta final en una etapa separada de adición.
Este enfoque de cálculo (aunque no necesariamente con la disposición explícita de la cuadrícula) también se conoce como algoritmo de productos parciales. Su esencia es el cálculo de las multiplicaciones simples por separado, dejando toda la suma para la etapa final de reunión.