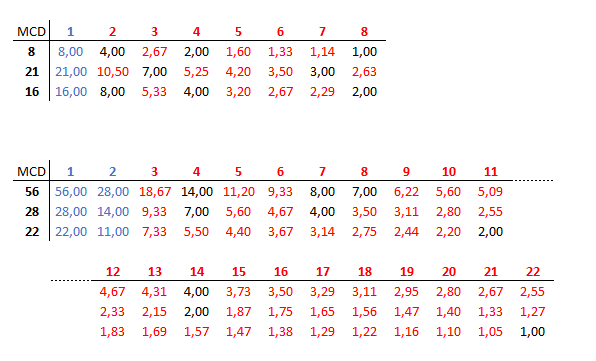
Multiplo comun divisor

Ggplot2 múltiples gráficos en el mismo gráfico

Aunque subplot() acepta un número arbitrario de objetos de trazado, pasar una lista de trazados puede ahorrar código redundante cuando se trata de un gran número de trazados. Por ejemplo, puede compartir el eje x utilizando shareX, establecer el ID del eje y especificar el número de filas con nrows.
En cualquier parte de esta página que veas fig, puedes mostrar la misma figura en una aplicación Dash for R pasándola al argumento figure del componente Graph del paquete incorporado dashCoreComponents así:

Ggarrange

## # … con 290 filas másPuede convertir esto en un marco de datos más largo donde el número de la pregunta se almacena en una columna y la respuesta se almacena en una columna separada:datos_largos <- datos_de_la_encuesta %>%.
## # … con 1.790 filas másNi siquiera necesita almacenar los datos del ‘formulario largo’ como una variable separada. Si no vas a utilizar los datos de esta forma para nada más, es más sencillo pasar los datos directamente a ggplot2. Aquí utilizo la función facet_wrap() para trazar cada pregunta en un panel separado, de modo que podamos ver la distribución de todas las preguntas a la vez:survey_data %>%
labs(x = “Respuesta (en una escala de 1 a 5)”, y = “Número de encuestados”)Puedes utilizar la pregunta como factor en cualquier otro lugar donde utilizarías una variable categórica con ggplot. Por ejemplo, puede hacer algunos gráficos de caja:datos_de_la_encuesta %>%
labs(x = “Pregunta”, y = “Respuesta (en una escala de 1 a 5)”)Esto es también una buena demostración de cómo los gráficos de caja son raramente la mejor manera de presentar los datos de la escala Likert.Cualquier otra variable se mantiene después de llamar a pivot_longer() , por lo que puede, por ejemplo, comparar las respuestas a las preguntas de la encuesta en base a una variable demográfica:survey_data %>%

Matematicas 2 primaria

Ggplot2 múltiples parcelas mismos ejes

Yutaka Ohsawa y Masao Sakauchi, A New Tree Type Data Structure with Homogeneous Nodes Suitable for a Very Large Spatial Database, Proc. Sixth International Conference on Data Engineering, February 5-9, 1990, Los Angeles, California, USA, pages 296-303.
Poner en orden los elementos comparando el elemento actual con el anterior. Si están en orden, se pasa al siguiente elemento (o se detiene si se llega al final). Si no están en orden, intercambia los elementos y pasa al elemento anterior. Si no hay ningún elemento anterior, se pasa al siguiente.
La complejidad es O(n2) para datos arbitrarios, pero se aproxima a O(n) si la lista está casi en orden al principio. Esto puede ser visto como una ordenación por inserción que sólo mantiene la pista del elemento actual. Después de haber movido un elemento hacia atrás en su lugar, “camina” hacia adelante, comprobando el orden de los elementos a medida que avanza, hasta que llega al siguiente elemento está fuera de lugar, que está más allá de donde el progreso dejó. Esto puede verse como una ordenación de burbujas bidireccional que invierte inteligentemente la dirección, en lugar de hacer pases completos.

Ggplot múltiples parcelas

Utilizamos gcd para calcular el máximo común divisor de dos números, y lcm para el mínimo común múltiplo de un conjunto arbitrario de números, pero hay que tener en cuenta que para lcm tenemos que cargar primero el paquete functs.
Cuando los métodos algebraicos son imposibles de aplicar, podemos hacer uso de rutinas numéricas. La biblioteca mnewton puede resolver ecuaciones y sistemas de ecuaciones por el método de Newton. Llamamos a la función mnewton con tres argumentos: la lista de ecuaciones, la lista de incógnitas y las coordenadas del punto semilla.
La resolución de desigualdades requiere el paquete fourier_elim. Primero resolvemos una desigualdad lineal con una sola incógnita. La función fourier_elim necesita dos argumentos, la lista de inecuaciones y la lista de incógnitas.
He aquí un ejemplo de cómo definir una nueva función en Maxima. Queremos escribir una función para calcular el módulo de un vector; vea que las funciones se definen mediante el operador :=. Bien, no te preocupes si no entiendes la parte interna de la función.
Cuando no se pueden aplicar métodos simbólicos, podemos hacer uso de algunas rutinas numéricas. Una de ellas es quad_qag; necesita cinco argumentos, el integrando, la variable independiente, los dos límites de integración y un número entero entre 1 y 6, que es un parámetro del procedimiento (3 es una buena elección). Lo que obtenemos es una lista de números, el primero es el valor de la integral definida, y el segundo es una estimación del error.