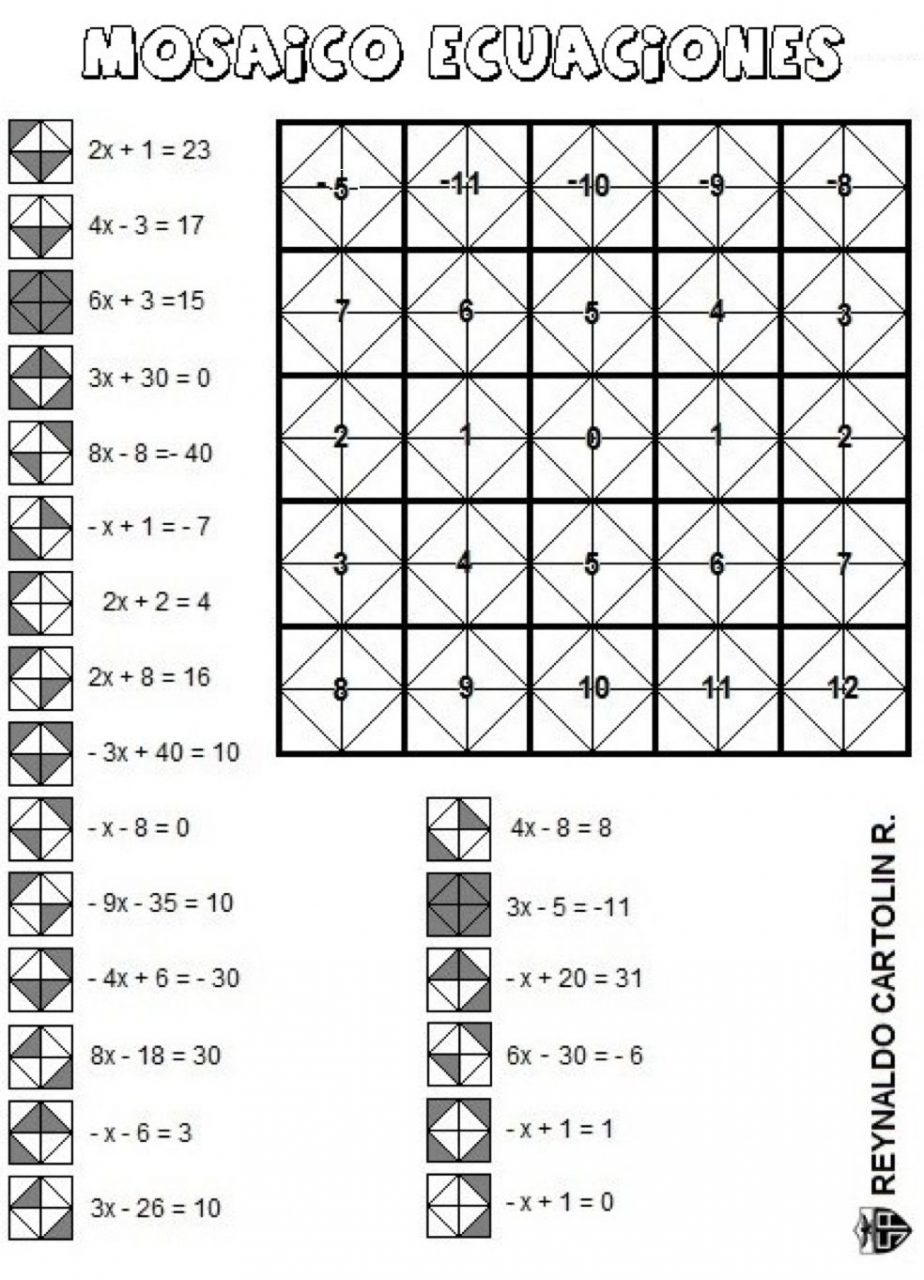
Juegos de ecuaciones de primer grado
Contenidos
Resolución de ecuaciones de primer grado en una variable
Al final de esta lección, los alumnos se familiarizarán con el lenguaje algebraico. Serán capaces de construir y resolver ecuaciones lineales. Además, resolverán problemas que impliquen la resolución de ecuaciones y descubrirán que estas ecuaciones se ven en la vida cotidiana.
Estas tareas han sido diseñadas para apoyar a los alumnos en el aprendizaje de la lectura, la escritura y la comprensión de problemas de palabras; repasar el vocabulario o hablar sobre un problema matemático que hayan resuelto. Estas tareas se detallan en “Materiales”.
Se trata de una tarea creativa en la que los alumnos se acercan a problemas reales. Además, serán capaces de utilizar la terminología adecuada con precisión y fluidez para explicar los procedimientos matemáticos a sus compañeros.
Se busca una metodología intuitiva y motivadora que promueva el aprendizaje mediante el descubrimiento de los conceptos a partir de conocimientos y experiencias personales. De este modo, los alumnos serán capaces de encontrar soluciones a los problemas y aprenderán a pensar. Esperamos que puedan descubrir conceptos y no sólo almacenarlos. Por ello, promovemos clases activas con actividades que hagan pensar y preguntar a los alumnos.
Respuestas de ecuaciones e inecuaciones de primer grado
Veamos ahora qué es una ecuación de primer grado y cómo resolver ecuaciones de primer grado de todo tipo: con paréntesis, con denominadores y con paréntesis y denominadores a la vez, con ejercicios resueltos paso a paso.
En esta ecuación, en el primer miembro tenemos la incógnita elevada a 2 y elevada a 3. En el segundo miembro la incógnita está elevada a 1. Recuerda que si la incógnita no tiene exponente significa que está elevada a 1:
Veamos un ejemplo de cómo se resuelven las ecuaciones sencillas de primer grado. Si entendemos perfectamente este tipo de ecuaciones, será más fácil comprender cómo se resuelven otras ecuaciones de primer grado más complicadas (con paréntesis, denominadores, potencias…).
Mediante la transposición de términos, tenemos que pasar los términos que llevan x al primer miembro y los números que no llevan x al segundo miembro. Los términos que ya están en el miembro correspondiente no deben tocarse.
Ahora, reescribimos el primer miembro, con los términos con x ya recolocados y el 14 que ya está en el segundo miembro. Lo único que tenemos que hacer es pasar el 2, que es ADDING y pasa HOLDING al segundo miembro:
Ejercicios de ecuaciones de primer grado pdf
serie de libros (BSPS, volumen 151)ResumenUna de las cuestiones más interesantes de la historia temprana del álgebra es la de la formación de los métodos para resolver las ecuaciones indeterminadas de primer grado. En la historiografía tradicional dichos métodos se asocian principalmente a las tradiciones matemáticas china e india. El hecho de que el Teorema del Resto se denomine comúnmente “Teorema del Resto Chino” en casi todos los libros de texto sobre la Teoría de los Números, expresa notablemente el punto de vista tradicional. Lo mismo ocurre con el llamado problema de las “cien aves”, cuyos orígenes también se reducen a la tradición matemática china.1 Palabras claveEcuación diofantina Teorema chino del resto Número propio Algoritmo euclidiano Tradición matemática
Ecuación cúbica
Las ecuaciones son de primer grado cuando pueden escribirse en la forma ax + b = c, donde x es una variable y a, b y c son constantes conocidas y a ¡a!=0. Discutimos las técnicas para resolver ecuaciones de primer grado en la sección 3.4 y de nuevo en la sección 3.5 al tratar las fórmulas. Además, encontrar las soluciones a las proporciones discutidas en las secciones 6.6 y 6.7 implica resolver ecuaciones de primer grado.
Este tema es uno de los más básicos e importantes para cualquier estudiante principiante de álgebra y se presenta de nuevo aquí para reforzarlo positivamente y como preparación para resolver una variedad de aplicaciones en las secciones 7.3, 7.4 y 7.5.
Hay exactamente una solución para una ecuación de primer grado en una variable. Esta afirmación puede demostrarse por el método de la contradicción. La prueba no se da aquí. Las ecuaciones que tienen más de una solución se discutirán en los capítulos 8, 9 y 10.
Esta última técnica tiene la ventaja de dejar sólo los coeficientes enteros y las constantes. Si hay más de una fracción, entonces cada término debe ser multiplicado por el LCM de los denominadores de las fracciones.