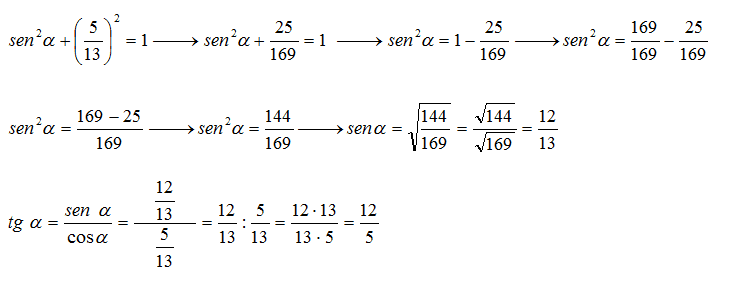Tangente
Base de la trigonometría: si dos triángulos rectos tienen ángulos agudos iguales, son semejantes, por lo que sus longitudes laterales son proporcionales. Las constantes de proporcionalidad se escriben dentro de la imagen: sin θ, cos θ, tan θ, donde θ es la medida común de cinco ángulos agudos.
En matemáticas, las funciones trigonométricas (también llamadas funciones circulares, funciones angulares o funciones goniométricas[1][2]) son funciones reales que relacionan un ángulo de un triángulo rectángulo con las relaciones de dos longitudes laterales. Se utilizan ampliamente en todas las ciencias relacionadas con la geometría, como la navegación, la mecánica de sólidos, la mecánica celeste, la geodesia y muchas otras. Se encuentran entre las funciones periódicas más sencillas y, como tales, también se utilizan ampliamente para estudiar los fenómenos periódicos mediante el análisis de Fourier.
Las funciones trigonométricas más utilizadas en las matemáticas modernas son el seno, el coseno y la tangente. Sus recíprocas son, respectivamente, la cosecante, la secante y la cotangente, que son menos utilizadas. Cada una de estas seis funciones trigonométricas tiene su correspondiente función inversa (llamada función trigonométrica inversa), y también un equivalente en las funciones hiperbólicas[3].
Ver más
La identidad trigonométrica pitagórica, también llamada simplemente identidad pitagórica, es una identidad que expresa el teorema de Pitágoras en términos de funciones trigonométricas. Junto con las fórmulas de suma de ángulos, es una de las relaciones básicas entre las funciones seno y coseno.
Cualquier triángulo semejante tiene la propiedad de que si seleccionamos el mismo ángulo en todos ellos, la razón de los dos lados que definen el ángulo es la misma independientemente del triángulo semejante que se seleccione, sin importar su tamaño real: las razones dependen de los tres ángulos, no de las longitudes de los lados. Así, para cualquiera de los triángulos rectángulos semejantes de la figura, la relación entre su lado horizontal y su hipotenusa es la misma, es decir, cos θ.
Como alternativa, se pueden emplear las identidades que se encuentran en Simetría trigonométrica, desplazamientos y periodicidad. Mediante las identidades de periodicidad podemos decir que si la fórmula es cierta para -π < θ ≤ π entonces es cierta para todo θ real. A continuación probamos el rango π/2 < θ ≤ π, para ello dejamos que t = θ – π/2, t estará ahora en el rango 0 < t ≤ π/2. Podemos entonces hacer uso de las versiones al cuadrado de algunas identidades de desplazamiento básicas (al elevar al cuadrado se eliminan convenientemente los signos menos):
Secante
Este artículo contiene posiblemente una investigación original. Por favor, mejórelo verificando las afirmaciones realizadas y añadiendo citas en línea. Las afirmaciones que sólo consisten en una investigación original deben ser eliminadas. (Noviembre de 2018) (Aprende cómo y cuándo eliminar este mensaje de la plantilla)
Este artículo puede ser demasiado largo para leer y navegar cómodamente. Por favor, considera dividir el contenido en subartículos, condensarlo o añadir subtítulos. Por favor, discute este tema en la página de discusión del artículo. (Enero 2021)
Todos los números trigonométricos -senos o cosenos de múltiplos racionales de 360°- son números algebraicos (soluciones de ecuaciones polinómicas con coeficientes enteros); además, pueden expresarse en términos de radicales de números complejos; pero no todos ellos son expresables en términos de radicales reales. Cuando lo son, son expresables más específicamente en términos de raíces cuadradas.
Todos los valores de los senos, cosenos y tangentes de los ángulos con incrementos de 3° son expresables en términos de raíces cuadradas, utilizando las identidades -la identidad de medio ángulo, la identidad de doble ángulo y la identidad de suma/resta de ángulos- y utilizando los valores de 0°, 30°, 36° y 45°. Para un ángulo de un número entero de grados que no sea múltiplo de 3° (π/60 radianes), los valores del seno, coseno y tangente no pueden expresarse en términos de radicales reales.
Arccosina
Este artículo necesita citas adicionales para su verificación. Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables. El material sin fuente puede ser cuestionado y eliminado.Buscar fuentes: “Prosthaphaeresis” – noticias – periódicos – libros – erudito – JSTOR (mayo de 2019) (Aprende cómo y cuándo eliminar este mensaje de la plantilla)
La prostaféresis (del griego προσθαφαίρεσις) fue un algoritmo utilizado a finales del siglo XVI y principios del XVII para multiplicar y dividir de forma aproximada utilizando fórmulas de la trigonometría. Durante los 25 años que precedieron a la invención del logaritmo en 1614, fue la única forma conocida de aplicación general para aproximar productos rápidamente. Su nombre proviene del griego prótesis (πρόσθεσις) y aféresis (ἀφαίρεσις), que significan suma y resta, dos pasos del proceso[1][2].
En la Europa del siglo XVI, la navegación celeste de los barcos en viajes largos dependía en gran medida de las efemérides para determinar su posición y rumbo. Estas voluminosas cartas preparadas por los astrónomos detallaban la posición de las estrellas y los planetas en distintos momentos. Los modelos utilizados para calcularlas se basaban en la trigonometría esférica, que relaciona los ángulos y las longitudes de arco de los triángulos esféricos (véase el diagrama de la derecha) mediante fórmulas como