Ejemplos de prisma

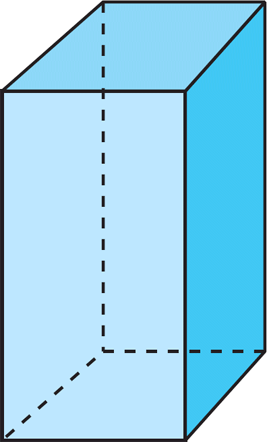
Ejemplos de prismas rectangulares

En geometría, un prisma es un poliedro que comprende una base poligonal de n lados, una segunda base que es una copia trasladada (movida rígidamente sin rotación) de la primera, y otras n caras, necesariamente todas paralelogramos, que unen los lados correspondientes de las dos bases. Todas las secciones paralelas a las bases son traslaciones de las mismas. Los prismas reciben el nombre de sus bases; por ejemplo, un prisma de base pentagonal se llama prisma pentagonal. Los prismas son una subclase de los prismatoides.
Como muchos términos geométricos básicos, la palabra prisma (griego: πρίσμα, romanizado: prisma, lit. ‘algo aserrado’) se utilizó por primera vez en los Elementos de Euclides. Euclides definió el término en el libro XI como “una figura sólida contenida por dos planos opuestos, iguales y paralelos, mientras que el resto son paralelogramos”. Sin embargo, esta definición ha sido criticada por no ser lo suficientemente específica en relación con la naturaleza de las bases, lo que causó confusión entre los escritores de geometría posteriores[3][4].
El volumen de un prisma es el producto del área de la base por la distancia entre las dos caras de la base, o la altura (en el caso de un prisma no recto, nótese que se trata de la distancia perpendicular).

Cuboide

Un prisma es una figura sólida tridimensional con dos caras paralelas, llamadas bases, que son polígonos congruentes, y caras planas laterales que son rectángulos en un prisma recto, y son paralelogramos en un prisma oblicuo.
En un prisma recto, las bases congruentes (trasladadas) aparecerán directamente una encima de la otra cuando el prisma esté asentado sobre su base. Los segmentos de línea que unen los correspondientes puntos extremos de cada base son congruentes, son paralelos entre sí y son perpendiculares a las bases. Estos segmentos paralelos se denominan aristas laterales y representan la altura del prisma. Las caras laterales de un prisma recto son rectángulos.
Un prisma oblicuo es aquel que parece inclinarse en un ángulo. En un prisma oblicuo, las bases congruentes NO aparecerán directamente una encima de la otra cuando el prisma esté asentado sobre su base. Los segmentos de línea que unen los correspondientes puntos extremos de cada base siguen siendo congruentes y paralelos entre sí, pero NO son perpendiculares a las bases y NO representan la altura del prisma. La altura de un prisma oblicuo no se encuentra en una arista lateral ni es paralela a ella. Las caras laterales de un prisma oblicuo son paralelogramos.

Aerle.es

Área del prisma

En el CSG, los jugadores se limitan a elegir repetidamente entre las acciones de “piedra”, “papel” y “tijera”, por lo que los módulos de los jugadores no contienen ninguna variable y las guardias y actualizaciones de los comandos correspondientes a la elección de estas acciones son el predicado true.
Como los dos jugadores tienen el mismo comportamiento, especificamos el segundo jugador cambiando el nombre del módulo del primero. Dado que un requisito para especificar CSGs en el lenguaje PRISM es que las acciones de los jugadores sean distintas, utilizamos el índice del jugador en las etiquetas de las acciones, por ejemplo, utilizamos r1 y r2 para denotar a los jugadores 1 y 2 que eligen la acción “roca” respectivamente.
Para registrar qué jugador gana cada ronda del juego hay un módulo adicional de grabación que no está bajo el control de ningún jugador. Los comandos de este módulo están etiquetados por listas de acciones correspondientes a las elecciones de los dos jugadores. El orden de las listas de acciones no es importante ya que las acciones de los diferentes jugadores son distintas (los únicos requisitos de las listas de acciones son cuando aparecen en un módulo bajo el control de un jugador y en este caso la primera acción debe ser la acción de ese jugador). Como el módulo no está bajo el control de ningún jugador, se requiere que sea determinista, lo que se cumple ya que para cada posible elección de acciones por parte de los jugadores sólo hay un comando etiquetado con la lista correspondiente.

El cilindro es un prisma

Un prisma recto es un sólido geométrico que tiene como base un polígono y caras verticales perpendiculares a la base. La base y la superficie superior tienen la misma forma y tamaño. Se llama prisma “recto” porque los ángulos entre la base y las caras son ángulos rectos.
Un prisma triangular tiene como base un triángulo, un prisma rectangular tiene como base un rectángulo y un cubo es un prisma rectangular con todas sus caras de igual longitud. Un cilindro es otro tipo de prisma recto cuya base es un círculo. A continuación se dan ejemplos de prismas rectos: un prisma rectangular, un cubo, un prisma triangular y un cilindro.
Un recipiente de chocolate muy popular es un prisma triangular recto equilátero con lados de \(\text{34}\️) \(\text{mm}\️). La caja tiene una longitud de \(\text{170}\️) \️. Calcula la superficie de la caja (al centímetro cuadrado más cercano).
Gordon compra un depósito de agua cilíndrico para recoger el agua de lluvia de su tejado. Descubre una lata llena de pintura verde en su garaje y decide pintar el depósito (no la base). Si utiliza 250 ml de pintura para cubrir 1 ml de pintura, ¿tendrá suficiente pintura verde para cubrir el tanque con una sola capa de pintura?