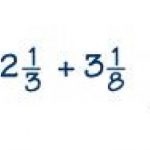Que son las fracciones equivalentes ejemplos
Contenidos
Cómo hacer fracciones equivalentes
Este artículo fue escrito por David Jia. David Jia es un tutor académico y el fundador de LA Math Tutoring, una empresa de tutoría privada con sede en Los Ángeles, California. Con más de 10 años de experiencia en la enseñanza, David trabaja con estudiantes de todas las edades y grados en diversas materias, así como en el asesoramiento de admisión a la universidad y la preparación de exámenes para el SAT, ACT, ISEE, y más. Después de obtener una puntuación perfecta de 800 en matemáticas y 690 en inglés en el SAT, David fue galardonado con la beca Dickinson de la Universidad de Miami, donde se graduó con una licenciatura en Administración de Empresas. Además, David ha trabajado como instructor de videos en línea para compañías de libros de texto como Larson Texts, Big Ideas Learning y Big Ideas Math.
Dos fracciones son equivalentes si tienen el mismo valor. Saber cómo convertir una fracción en una equivalente es una habilidad matemática esencial que es necesaria para todo, desde el álgebra básica hasta el cálculo avanzado. Este artículo cubrirá varias maneras de calcular fracciones equivalentes, desde la multiplicación y división básicas hasta métodos más complejos para resolver ecuaciones de fracciones equivalentes.
Fracción equivalente de 3/4
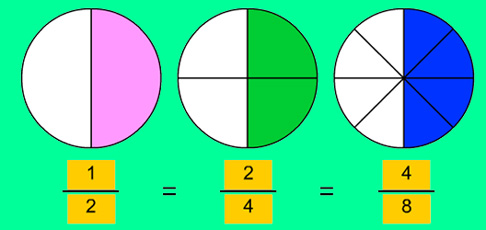
Fracciones equivalentes: Se define como las fracciones que tienen numeradores y denominadores diferentes pero el mismo valor. Podemos decir que 2/6, 3/9 y 4/12 son las fracciones equivalentes que tienen números diferentes pero la misma proporción. Para obtener una fracción equivalente, podemos multiplicar o dividir el numerador y el denominador con el mismo número. No hay que sumar ni restar para encontrar fracciones equivalentes.
Puedes consultar las soluciones NCERT para el capítulo 2 de matemáticas de la clase 7 sobre fracciones y decimales para una mejor comprensión de los conceptos. Hemos proporcionado información detallada sobre las fracciones equivalentes en este artículo, sigue leyendo para conocer su definición y ejemplos.
La fracción equivalente se define como la fracción que tiene diferente numerador y denominador pero que representa el mismo valor. Dos o más fracciones son equivalentes si son iguales a la misma fracción cuando se multiplican. Por ejemplo, la fracción equivalente de 1/2 es 2/4, 3/6, 4/8. Podemos decir que tienen el mismo valor independientemente de su numerador y denominador.
Calculadora de fracciones equivalentes
Las fracciones son uno de los temas básicos más importantes de las matemáticas y los estudiantes deben entender cómo realizar operaciones con fracciones, como sumar y restar fracciones y multiplicar fracciones. Pero, antes de que los estudiantes puedan entender las fracciones a un nivel avanzado, es fundamental que tengan un sólido conocimiento de las fracciones equivalentes.En la vida real, a menudo tratamos diferentes valores que pueden considerarse equivalentes o iguales entre sí. Por ejemplo, sabemos que 60 minutos equivalen a 1 hora y también sabemos que 16 onzas equivalen a una libra. En cada caso, estamos expresando la misma cantidad de tiempo o peso de dos maneras diferentes que son intercambiables.Esta idea de expresar dos valores iguales de diferentes maneras es similar en matemáticas cuando se trata de fracciones equivalentes.Esta guía completa de fracciones equivalentes proporcionará un tutorial paso a paso sobre cómo entender las fracciones equivalentes y cómo encontrarlas.Primero, vamos a empezar con la definición de fracciones equivalentes:Definición de matemáticas: Fracciones equivalentesLas fracciones equivalentes son fracciones que tienen la s
Definición de fracciones equivalentes
En el lado izquierdo \( b \) es un factor común al numerador y al denominador y, por lo tanto, se puede simplificar. En el lado derecho \( d \) es un factor común al numerador y al denominador y, por lo tanto, se puede simplificar. De ahí que obtengamos la igualdad
Una forma de responder a esta pregunta es utilizar la multiplicación cruzada que ya hemos utilizado en el ejemplo 1. Otra forma es demostrar que una fracción se obtiene a partir de la segunda mediante la multiplicación o división del numerador y el denominador por el mismo número entero.
La fracción dada \( \dfrac{1}{3}{3}) es equivalente a la fracción \( \dfrac{3}{9}{9}) de la parte c) porque el producto cruzado de las dos fracciones \( 1 \️ 9 = 3 \️ 3) produce un enunciado verdadero después del cálculo: \( 9 = 9 \)
La fracción dada \( \dfrac{5}{9} \) es equivalente a la fracción \( \dfrac{10}{18} \) de la parte d) porque el producto cruzado de las dos fracciones \( 5 \times 18 = 9 \times 10 \) produce una afirmación verdadera después del cálculo: \( 90 = 90 \).
La fracción dada \( \dfrac{-5}{7} \) es equivalente a la fracción \( \dfrac{-15}{21} \) de la parte a), porque el producto cruzado de las dos fracciones \( -5 \times 21 = 7 \times (-15) \) produce una afirmación verdadera después del cálculo: \( -105 = -105 \)