Concepto de media en matematicas

Media geométrica

En el lenguaje coloquial, una media es un único número tomado como representativo de una lista no vacía de números. En diferentes contextos se utilizan diferentes conceptos de media. A menudo, “promedio” se refiere a la media aritmética, la suma de los números dividida entre cuántos números se están promediando. En estadística, la media, la mediana y la moda se conocen como medidas de tendencia central, y en el uso coloquial cualquiera de ellas podría llamarse valor medio.
Otra propiedad universal es la monotonicidad: si dos listas de números A y B tienen la misma longitud, y cada entrada de la lista A es al menos tan grande como la entrada correspondiente de la lista B, entonces el promedio de la lista A es al menos como el de la lista B. Además, todos los promedios satisfacen la homogeneidad lineal: si todos los números de una lista se multiplican por el mismo número positivo, entonces su promedio cambia por el mismo factor.
En algunos tipos de promedios, los elementos de la lista tienen asignadas diferentes ponderaciones antes de determinar la media. Entre ellos se encuentran la media aritmética ponderada, la media geométrica ponderada y la mediana ponderada. Además, en algunos tipos de media móvil, el peso de un elemento depende de su posición en la lista. Sin embargo, la mayoría de los tipos de media satisfacen la insensibilidad a la permutación: todos los elementos cuentan por igual para determinar su valor medio y sus posiciones en la lista son irrelevantes; la media de (1, 2, 3, 4, 5) es la misma que la de (3, 2, 5, 4, 1).

Cálculo de la media

En el lenguaje coloquial, una media es un único número tomado como representativo de una lista no vacía de números. En diferentes contextos se utilizan diferentes conceptos de media. A menudo, “promedio” se refiere a la media aritmética, la suma de los números dividida entre cuántos números se están promediando. En estadística, la media, la mediana y la moda se conocen como medidas de tendencia central, y en el uso coloquial cualquiera de ellas podría llamarse valor medio.
Otra propiedad universal es la monotonicidad: si dos listas de números A y B tienen la misma longitud, y cada entrada de la lista A es al menos tan grande como la entrada correspondiente de la lista B, entonces el promedio de la lista A es al menos como el de la lista B. Además, todos los promedios satisfacen la homogeneidad lineal: si todos los números de una lista se multiplican por el mismo número positivo, entonces su promedio cambia por el mismo factor.
En algunos tipos de promedios, los elementos de la lista tienen asignadas diferentes ponderaciones antes de determinar la media. Entre ellos se encuentran la media aritmética ponderada, la media geométrica ponderada y la mediana ponderada. Además, en algunos tipos de media móvil, el peso de un elemento depende de su posición en la lista. Sin embargo, la mayoría de los tipos de media satisfacen la insensibilidad a la permutación: todos los elementos cuentan por igual para determinar su valor medio y sus posiciones en la lista son irrelevantes; la media de (1, 2, 3, 4, 5) es la misma que la de (3, 2, 5, 4, 1).

Matematicas 6 primaria

Comentarios

La media, la mediana y la moda son tres tipos de “promedios”. Hay muchos “promedios” en estadística, pero estos son, creo, los tres más comunes, y son ciertamente los tres con los que es más probable que te encuentres en tus cursos de preestadística, si es que el tema surge.
La “media” es el “promedio” al que estás acostumbrado, donde sumas todos los números y luego los divides entre el número de números. La “mediana” es el valor “medio” de la lista de números. Para encontrar la mediana, los números tienen que estar ordenados numéricamente de menor a mayor, por lo que es posible que tengas que reescribir tu lista antes de poder encontrar la mediana. La “moda” es el valor que aparece con más frecuencia. Si ningún número de la lista se repite, entonces no hay moda para la lista.
Nota: La fórmula para encontrar la mediana es “([el número de puntos de datos] + 1) ÷ 2”, pero no tienes que usar esta fórmula. Puedes simplemente contar desde ambos extremos de la lista hasta que te encuentres en el medio, si lo prefieres, especialmente si tu lista es corta. Cualquiera de las dos formas funcionará.

Definición de media

MediaLa media es la más común, conocemos la media, comparando el resumen de valores. Es la suma de todos los números dividida por el número de sumandos o encuestados.Ejemplo: Las puntuaciones de diez alumnos son 82, 85, 79, 78, 89, 87, 88, 89, 75 y 77. ¿Cuál es la media? ¿Cuál es la media? Media =(suma de todos los números ) / (número de encuestados)Media = (82 + 85 + 79 + 78 + 89 + 87 + 88 + 89 + 75 + 77 ) / 10Media =( 829) / 10Media = 82,9 son 83
MedianaLa mediana es el valor del término medio cuando se ordenan los datos. Puede estar en orden ascendente o descendente. Para calcular la mediana, recuerda lo siguiente:a. Ordena los números en orden numérico.b. Si los elementos son un número impar, la mediana está en el medio. c. Si los elementos son un número par, calcula el número central.
Mediana con el número imparEjemplo:El número de libros que los alumnos toman prestados cada día son 63, 31, 42, 54 y 50.a. Ordena lo siguiente 31, 42, 50, 54, 63.b. El número de elementos es impar porque hay 5 elementos. La mediana es 50.
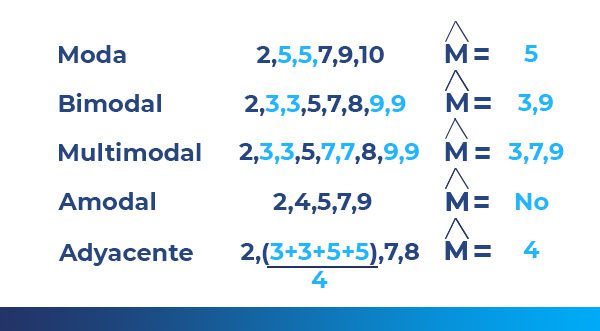
ModoSe denomina modo a los números más frecuentes que se dan en el conjunto de datos. Ejemplo: Las puntuaciones de diez estudiantes son 82, 85, 79, 78, 89, 87, 88, 89, 75 y 77. ¿Cuál es la moda? La moda es 89.