Cosecante
Has visto bastantes identidades trigonométricas en las últimas páginas. Es conveniente tener un resumen de ellas como referencia. Estas identidades se refieren en su mayoría a un ángulo denominado θ, pero hay algunas que implican dos ángulos, y para ellas, los dos ángulos se denominan α y β.
Además: curiosamente, estas identidades de producto se utilizaban antes de que se inventaran los logaritmos para realizar la multiplicación. Así es como se puede utilizar la segunda. Si quieres multiplicar x por y, utiliza una tabla para buscar el ángulo α cuyo coseno es x y el ángulo β cuyo coseno es y. Busca los cosenos de la suma α + β. y de la diferencia α – β. Haz la media de esos dos cosenos. ¡Obtienes el producto xy! Tres búsquedas en la tabla, y el cálculo de una suma, una diferencia y un promedio en lugar de una multiplicación. Tycho Brahe (1546-1601), entre otros, utilizó este algoritmo conocido como prosthaphaeresis.
Sin, cos tan calculadora
¿Sabes lo que se dicen dos ángulos que viven dentro del mismo triángulo rectángulo? El primer ángulo dice: “Oye Thelma (¿o es Theta?), no quiero salirme por la tangente, pero ¿cuál es tu seno?”. A lo que el segundo ángulo responde: “Phil (¿o es Phi?), no sé por qué te molestas en preguntar, ¡mi seno es obviamente el mismo que tu coseno!”.
Vale, quizá no sea el mejor chiste del mundo, pero una vez que entiendes los senos y los cosenos, es bastante divertido. Por supuesto, eso significa que si no conoces la diferencia entre un seno y un coseno, actualmente te has quedado fuera en el frío metafórico.
Cuando hablamos del mundo de la trigonometría, aprendimos que la parte de las matemáticas llamada trigonometría se ocupa de los triángulos. Y, en particular, es la parte de las matemáticas que se ocupa de averiguar la relación entre los tres lados y los tres ángulos que componen cada triángulo.
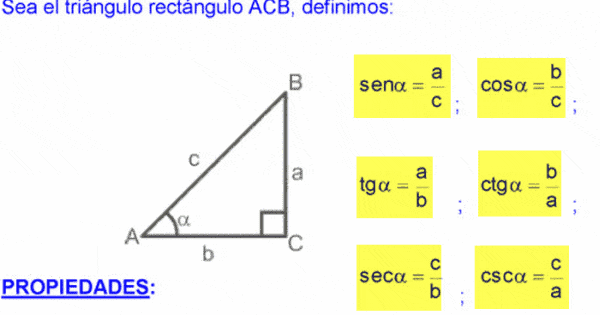
Nos interesa especialmente el tipo especial de triángulos conocido como triángulos rectángulos. Todos los triángulos rectángulos tienen un ángulo de 90 grados (como la esquina de un cuadrado o un rectángulo) y dos ángulos que oscilan entre 0 y 90 grados (como veremos más adelante, la suma de los tres ángulos es de 180 grados).
Secante
Hay muchas otras herramientas útiles cuando se trata de problemas de trigonometría. Echa un vistazo a las dos leyes trigonométricas más populares: las calculadoras de la ley de los senos y la ley de los cosenos, que ayudan a resolver cualquier tipo de triángulo. Si quieres leer más sobre las funciones trigonométricas, ve a nuestras herramientas dedicadas:
La trigonometría tiene multitud de aplicaciones: desde problemas de la vida cotidiana como el cálculo de la altura o la distancia entre objetos hasta el sistema de navegación por satélite, la astronomía y la geografía. Además, las funciones seno y coseno son fundamentales para describir fenómenos periódicos: gracias a ellas, podemos describir movimientos oscilatorios (como un simple péndulo) y ondas como el sonido, la vibración o la luz.
Para encontrar las funciones trigonométricas de un ángulo, introduce el ángulo elegido en grados o radianes. Debajo de la calculadora aparecerán las seis funciones trigonométricas más populares: tres básicas: seno, coseno y tangente, y sus recíprocas: cosecante, secante y cotangente. Además, si el ángulo es agudo, se mostrará el triángulo rectángulo, lo que puede ayudarte a entender cómo se pueden interpretar las funciones.Calculadora de trigonometría como herramienta para resolver el triángulo rectángulo
Seno
Dibuja una circunferencia de radio 1 unidad. El punto P con coordenadas (x , y) se mueve alrededor de la circunferencia del círculo. P forma un ángulo θ con el eje x positivo. El ángulo aumenta a medida que P gira en sentido contrario a las agujas del reloj. Para cualquier ángulo θ el seno, el coseno y la tangente vienen dados por las coordenadas de P.
La curva del seno modela muchos fenómenos naturales, como las ondas de sonido y de luz. Debido a que se repite cada 360°, la gráfica se describe como periódica con período de 360°. (Las otras curvas son igualmente periódicas con períodos de 360° para el coseno y de 180° para la tangente). Obsérvese que la curva de la tangente tiene una forma diferente y que a 90°, 270°, 450°, etc., el valor de la tangente es infinito y, por tanto, no puede representarse.
La gráfica de sin θ oscila entre 01 y !1. Esto significa que la amplitud de la curva senoidal es 1. La amplitud se puede cambiar multiplicando sin θ por un número, por ejemplo 4. La gráfica de 4 sin θ se muestra en la Figura 4.